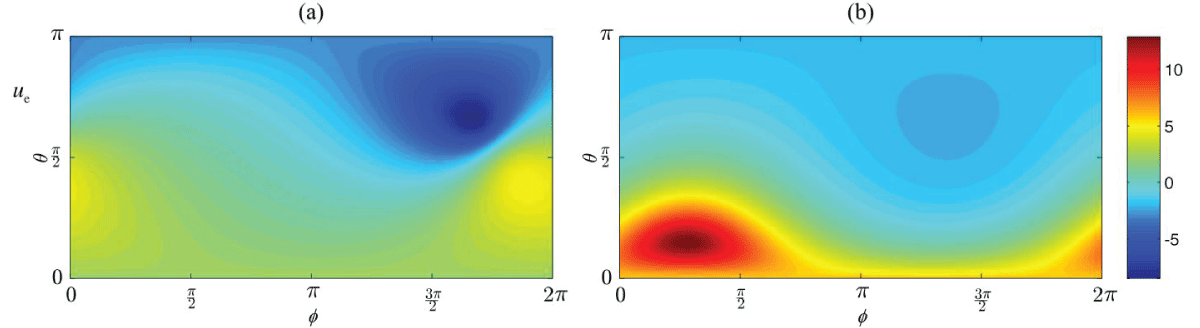
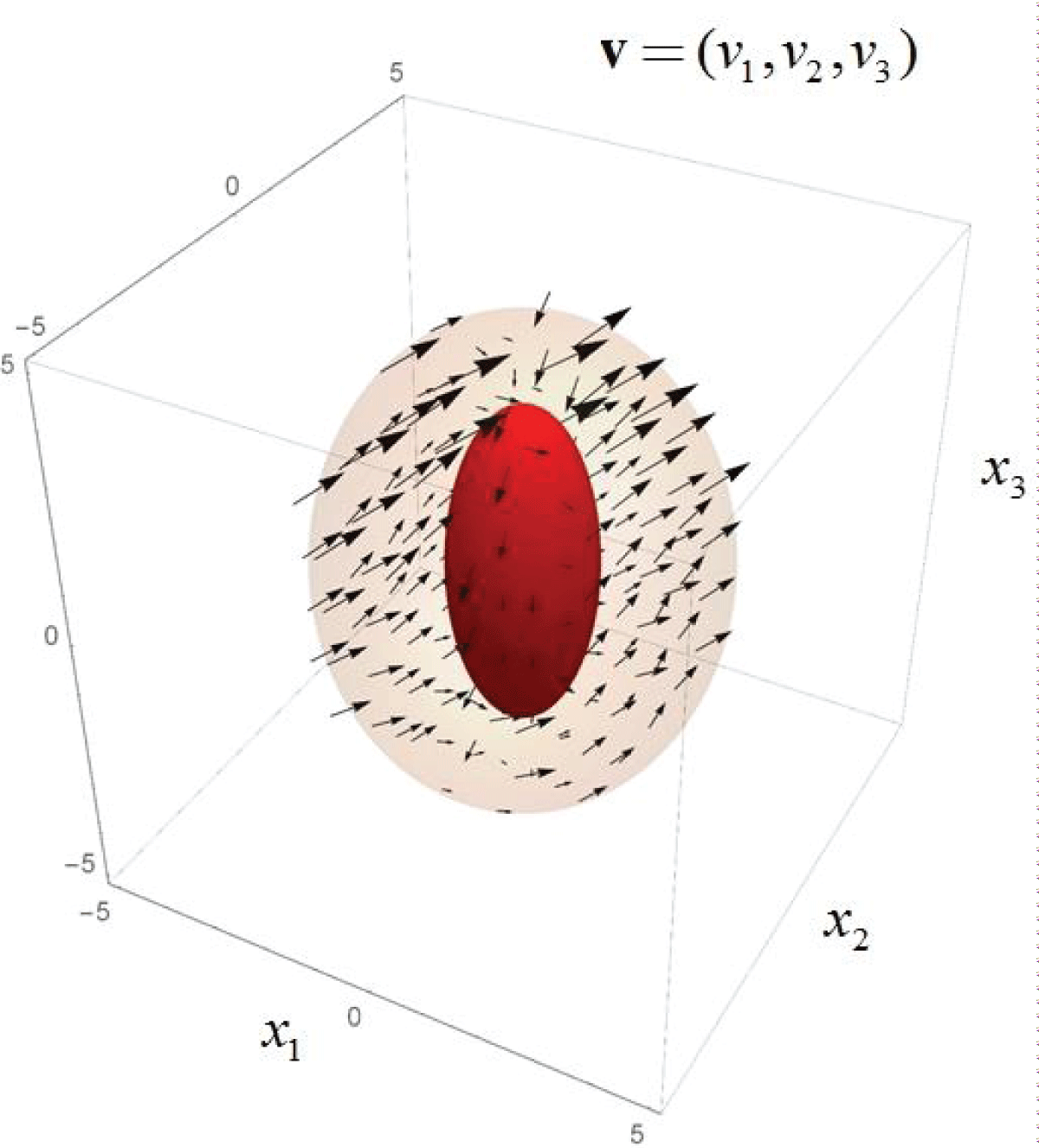
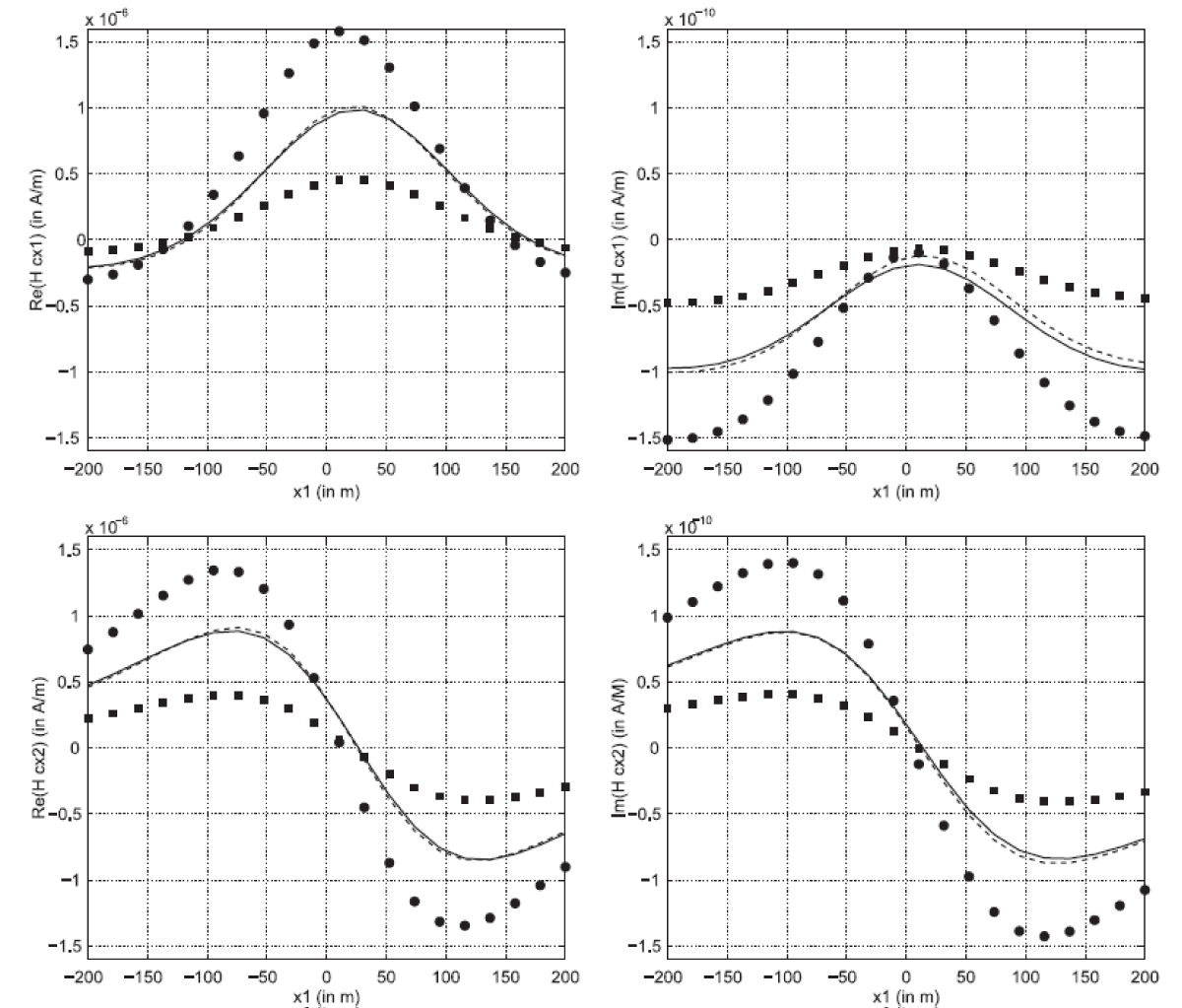
Abstract
Many applications in science, engineering, and modern technology require the solution of boundary value problems for genuine three-dimensional objects. These objects often are of or can be approximated by, an ellipsoidal shape, where the three ellipsoidal semiaxes correspond to three independent degrees of freedom. The triaxial ellipsoid represents the sphere of any anisotropic space and for this reason, it appears naturally in many scientific disciplines. Consequently, despite the complications of the ellipsoidal geometry and mainly its analysis, based on the theory of ellipsoidal harmonics, a lot of progress has been made in the solution of ellipsoidal boundary value problems, due to its general applicability. In this mini-review, we aim to present to the scientific community the main achievements towards the investigation of three such physical problems of medical, engineering and technological significance, those comprising intense research in (a) electroencephalography (EEG) and magnetoencephalography (MEG), (b) creeping hydrodynamics (Stokes flow) and (c) identification of metallic impenetrable bodies, either embedded within the Earth’s conductive subsurface or located into a lossless air environment. In this context, special expertise and particular skills are needed in solving open boundary value problems that incorporate the ellipsoidal geometry and the related harmonic analysis, revealing the fact that there still exists the necessity of involving with these issues.