Problem of Surface Waves on Water in Higher School Laboratory Workshop
Physics Applied SciencesReceived 24 Sep 2024 Accepted 21 Oct 2024 Published online 22 Oct 2024
ISSN: 2995-8067 | Quick Google Scholar

Received 24 Sep 2024 Accepted 21 Oct 2024 Published online 22 Oct 2024
Traditionally, in lecture courses on General Physics, the example of waves propagating on the water surface is used for the qualitative description of wave phenomena. At the same time, in corresponding laboratory courses, there are almost no quantitative tasks on the same topic, the purpose of which would be to measure the surface wave characteristics. The reason for this difference must be associated with the complexity of the physical mechanism of generation and propagation of waves on the water surface. In this work, a laboratory problem has been developed to measure the group velocity of circular waves traveling on the water surface. It uses a standard laboratory water tank equipped with a surface wave generator. The proposed experiment offers an opportunity for quantitative measurement of surface wave characteristics, a dispute of only qualitative observations of wave phenomena commonly found in current curricula, due to the introduction of two improvements. First, to produce the water waves’ rich in-contrast representations on a screen, the optimal generator amplitude is specially set for each experiment; and second, to measure the group wavelength, the device magnification is preliminary calculated based on the laws of geometric optics. The tests carried out have shown that the relative accuracy of these measurements is quite acceptable: within a few percent. The introduction of the problem of surface waves on water into the General Physics laboratory workshop for engineering specialties of technical universities will contribute to improving the quality of mastering the subject by students.
In lecture courses on General Physics the example of waves, propagating on the water surface is widely used for the qualitative description of wave phenomena. In contrast, in corresponding laboratory courses, there are almost no quantitative tasks aiming to measure various characteristics of such waves. The reason for this difference we associate with the complexity of the physical mechanism of formation and propagation of waves on the water surface.
In general, water waves are a mixture of longitudinal and transverse surface waves related to forces of surface tension and gravity, respectively. They are deformations of the water surface propagating with the wave velocity, while the water molecules remain at the same positions on average. Energy, however, moves with the wave velocity as well. There are known so-called deep- and shallow-water waves. The distinction between them is determined by the ratio of the water’s depth d to the half-wavelength λ/2.
When d >> λ/2, one has deep-water waves or short waves. They reveal the dispersion property, i.e. the velocity of deep-water waves depends on their wavelength. Every molecule of a deep-water wave moves in a circular orbit, the diameter of which decreases with the distance from the surface. The motion is felt down to a distance of ~λ, where the waves’ energy becomes negligible.
At d << λ/2 shallow-water waves or long waves arise. They show almost no dispersion. However, the velocity of shallow-water waves depends on the water’s depth. The molecules of a deep-water wave move in elliptic orbits.
In this paper, a laboratory problem is developed to measure by students the group velocity of deep-water surface waves at low frequencies. It uses a standard laboratory water tank equipped with a generator of circular surface waves. The tests carried out have shown that the relative accuracy of these measurements is quite acceptable: within a few percent. The introduction of the laboratory problem “Determination of Group Velocity of Surface Waves on Water” into the General Physics laboratory workshop for engineering specialties of technical universities will contribute to improving the quality of mastering the subject by students.
A huge number of studies are devoted to improving the quality of teaching physics and closely related issues of other natural sciences, as well as engineering and mathematics. In this brief review, we consider only a small part of the literature recently published on the problems, the solution of which is especially important for the engineering specialties of technical universities.
Starting from the US federal legislation specifying equitable access to education for all students at all levels of education, including postsecondary education, [1] explored how well the physics education research community has to serve students who inherently vary in their needs, abilities, and interests. Four research-based curricula (namely, Tutorials in Introductory Physics, Open Source Tutorials in Physics Sensemaking, Physics by Inquiry, and Next Generation Physical Science and Everyday Thinking) were compared with a universal design for learning framework originated in the education literature base. It was stated that if the physics education research community wants instructors to use high-quality, research-based curricula, curriculum developers should prioritize the support of all learners.
In the Italian education system, secondary students are confronted with the foundations of quantum physics during the final term (in the preuniversity year) of scientific high school. [2] wishing to illustrate the didactic suggestions focused on learning motivation that emerged during a long teaching experience, which could help to tackle the main problems found. In particular, experimental evidence of the undulatory nature of matter, postulated by De Broglie, and the uncertainty principle could conclude the path significantly. The experimental dimension can be further explored with activities to be carried out not only in the educational laboratory of the scientific high school but also in laboratories of universities and research institutions, adhering to guidance projects.
Factors that affect exclusively physical, virtual, and both Virtual-Physical (VP) and Physical-Virtual (PV) sequences of manipulatives were explored [3] within a Studio Physics environment, in which students actively work together to learn through real-world experimentation and simulation-based activities as well. Statistics show that comprehensive learning groups (i.e. any combination of PV or VP sequences) performed better than any other setting. The study also pinpoints the importance of the sequence for which virtual or physical experiments of some specific concepts are initially introduced to students.
Didactic design and outcomes in an educative program, involving several physics and mathematics university courses for engineers, based on the use and construction of widgets generated under Project Oriented Learning and Blended Learning methodologies was summarized in the work [4]. In this approach, the widgets generated by teachers are used by students to appropriate some basic concepts and then to generate their own widgets to develop complex thinking skills, applying related concepts but involving alternative situations. Mathtab and other widget developers were used to generate activities in terms of their capabilities and course requirements. Post-test results of students’ value perceptions indicated positive attitudes toward the use of widgets.
There were different kinds of activities – exhibitions, educational research, and sessions for students – involving the Laboratory of Mathematical Machines of the University of Modena e Reggio Emilia and its collection of instruments, the mathematical machines [5]. They are copies of historical instruments, constructed with an educational aim but also used in the popularization of mathematics.
The “Talk about Chemistry” (TAC) is a series of annual voluntary meetings to talk about current and stimulating chemistry topics and discuss how to teach and learn them [6]. TACs are the integrating actions involving undergraduates, new and senior chemistry teachers, and teacher educators as well. Their short speeches are clear and accessible, in order to encourage the audience’s participation. These activities provide simultaneously initial training and the continuous education of chemistry teachers. TACs require relatively little resources and organization but have a quite positive impact regarding the training of chemistry teachers.
It was identified that the majority of chemistry textbooks, both for high school and higher education, show the key physical-chemical concept of electronegativity in an ahistorical and decontextualized manner. In this perspective of teaching, the concept of electronegativity becomes inadequate to the reality into which it is inserted, because the information present in the textbooks, generally speaking, does not seek to explain the relation between electronegativity and other periodical properties of chemical elements. Besides, textbooks use only one (namely, Pauling’s) definition of electronegativity, not taking into account other possible approaches to the same concept. Such a strong standardization of characteristics shown in textbooks, from the point of view of [7], can lead students to conceptual errors. Thus, it is proposed that the treatment of the concept of electronegativity be performed within a historical context establishing connections between electronegativity and other physical/chemical concepts with which it is constituted in an inter-relational base.
There was investigated [8] the effect of molecular model sets on naming simple organic compounds with reference to the International Union of Pure and Applied Chemistry (IUPAC) system of naming. A quasi-experimental design using molecular model sets was used on students in form three science classes of senior high school. Analysis of the pre-test and post-test scores showed more improvement in the performance of the experimental group than the control group. A paired sample test, on responses of students’ attitudes, showed a statistically significant difference between the mean scores for the experimental group before and after the treatment. The study revealed that the integration of molecular model set approaches to teaching could help reduce, if not remove completely, the difficulties students face in naming organic compounds according to the IUPAC nomenclature. Furthermore, the study indicated that the integration of molecular model sets in teaching organic chemistry topics enhanced the students’ conceptual understanding. Moreover, the syllabus should not be loaded so that teachers would not concentrate on the theory aspect alone but would also include many practical lessons to improve chemistry teaching and learning in senior high schools.
In the paper [9], responding to 100 years of the Knudsen gauge, it was described as a corresponding laboratory exercise for high school physics students. The students were presented with the outline of the experiment, the necessary equations, and a collection of parts (including fiber suspension, heater, eddy current damper, mirror, and tension adjustment assembly) from which it is possible to build the Knudsen gauge and then take measurements to determine the pressure-force relationship and the pressure range over which the apparatus could provide useful results. The vacuum system applied a diffusion pump and a mercury McLeod gauge was used as the standard.
After reporting on the impact of students’ preconceptions on learning, the review [10] highlighted some existing studies on students’ misconceptions of electricity and magnetism. This paper also updated physics educators and researchers on conceptual assessments used to test students’ misconceptions about electricity and magnetism and suggested strategies for their remedying. Some educational implications and practical recommendations for effective teaching and learning in electricity and magnetism were also outlined.
The purpose of the study [11] was to review the postgraduate theses on physics education (in Turkey) to guide the teaching of the sound concept. Both conventional and contemporary approaches were found to have a positive effect on the achievement of the sound concept. However, students and teacher candidates, in general, were not able to relate their knowledge of sound to daily life and their level of knowledge was inadequate. The most important output of this study is the list of possible misconceptions or confusion about the concept of sound.
A characteristic of teaching and learning approaches used within the new concept of Learning-by-Being (LBB) was given [12]. The evolution of educational paradigms from Learning-by-Doing (LBD) and Learning-by-Understanding (LBU) toward LBB was analyzed. The basic idea of LBB is students’ ownership of cognitive goals, or the assumption of learning objectives, in other words – the intrinsic motivation of students. The school physics lab was examined as an example of a constructivist learning environment. The basic principles for its organization in a constructivist manner were enumerated as the provision of opportunities for students’ own thinking, giving students the freedom to identify solutions through verbalization of the problem, a necessity for teachers to know a priori concepts of students, their effort as a mandatory condition to achieve own interest.
If certain momentum is periodically transmitted to some point on the flat horizontal surface of a reservoir with homogeneous water, for example, from a ball that vibrates in the vertical direction, then the surface waves with a circular front appear. A reservoir is considered of “infinite depth” and “infinite area” if these wave disturbances due to their attenuation with travelling distance practically do not reach, respectively, the bottom and shores of the reservoir. In this case, there is no interference of the primary wave with waves reflected from the bottom and shores. On the surface of a reservoir of “infinite depth” and “infinite area” a monochromatic wave, which corresponds to a certain wavelength λ, propagates with velocity v called wave phase velocity.
Governing equations for monochromatic waves on the water surface can be found, e.g., in [13]. They lead the v = v(λ) dispersion relation for surface tension-gravity progressive waves on deep-water surface in the following form:
(1)
where, ρ is the water density, σ is the air-water interface tension coefficient, and g is the acceleration of gravity.
By the nature of the forces that return the surface of the water to its initial, i.e. undisturbed or equilibrium state, the water surface waves are distinguished as gravitational and capillary waves. They are determined, respectively, by the force of gravity and the force of the liquid surface tension. It is clear that in the above formula (1) in the sum under the square root, the first term corresponds to gravitational waves and the second to capillary waves. It is also seen that gravitational effects dominate at long wavelengths, while capillary ones – at short wavelengths.
Phase velocity reaches its minimum of
(2)
(3)
Note that ρ ≈ 1000 kg/m3, σ ≈ 0.0727 N/m, and g ≈ 9.81 m2/s, so that λmin ≈ 17 mm. Thus, for monochromatic surface waves, the water can be considered as deep if its depth satisfies the condition d >> 8.5 mm.
Also note that just at the minimum point (3), the values of the above two terms are equal each to other. Therefore, at relatively short wavelengths, λ << λmin, when waves on the water surface are mainly of a capillary nature their phase velocity is determined by the formula:
(4)
However, if the surface waves are rather long, λ >> λmin, then the gravitational mechanism of the waves’ formation prevails and the phase velocity is equal to:
(5)
However, in the general case, a wave propagating on the water reservoir's surface is not a monochromatic wave, but a group of monochromatic waves with a frequency of f equal to the oscillations frequency of the waves’ source (generator). Therefore, it is too important to determine the group velocity V of surface waves on water as a function of the group wavelength. We resolved [14] this problem in analytic form.
The group wavelength Λ can be defined as the distance that the intensity maximum of the group of waves travels during a period of oscillations. Consequently, the following relation holds:
(6)
Let us assume that the width ∆λ of the wavelength range, which accounts for the most part of the energy carried by a group of waves, is negligible if compared with the group wavelength: Δλ << Λ. In this case, the group of waves can be considered as a so-called wave packet and the velocity of movement of its intensity maximum, i.e. the group velocity of waves, can be calculated from the dispersion law v = v(λ) as follows:
(7)
Substituting into this general relation (7) the expression (1) written above for the dispersion law of surface waves on water, we obtain equality for the group velocity:
(8)
The extrema condition, , implies the biquadratic equation,
(9)
that determines the positions of the group velocity extrema. This equation has two real and two imaginary roots. From the real roots, one is positive and the other is negative. It is obvious that imaginary roots and a real negative root have no physical meaning. So that the group velocity minimum against the group wavelength corresponds to the real positive root:
(10)
At the group wavelength of Amin (10), the group velocity (8) reaches its minimum of
(11)
These theoretical results were experimentally verified by the test measurements.
Figure 1 shows the V – Λ dependence calculated for the above-stated curve parameters σ, and g. The corresponding coordinates of the weakly expressed minimum, (10) and (11), are Λmin = 43.6 mm and Vmin = 163 mm/s, respectively.
Note that for the relatively short and, therefore, mainly capillary nature waves, Λ << Λmin, the group velocity is equal to
(12)
whereas for the relatively long, i.e. mainly gravitational waves, Λ >> Λmin, we have:
(13)
In other words, in these two limiting cases the dispersity laws of the group velocity, respectively, are the corresponding phase velocity dispersity laws multiplied by factors 3/2 or 1/2.
Experimental setups useful for studying the waves on the water surface usually enable also experiments that are analogous to those carried out on other types, e.g., light, waves. Then, all the wave optics laws can be clearly demonstrated by means of water waves.
There were experimentally investigated [15] the large transient surface wave groups on water produced by the number of waves focused at one point in space and time. Results of measurements of the water surface elevation and the underlying kinematics were compared with theory. A wave flame was 20 long and 0.3 m wide and had a maximum working depth of 0.7 m. Waves period was 0.4 – 2.0 s. No reflected components could be tolerated within the working section. To achieve this aim, a large-block foam was installed to provide passive absorption of surface waves.
Dispute the fact that water surface waves are everyday phenomena they usually are not discussed in textbooks. The main reason is that surface waves are very different from most other waves in that their velocity is strongly dependent on the wavelength. When the wavelength is smaller, the wave velocity is affected by surface tension: by adding an agent to change the surface tension, it was noticed that the wave velocity increases with surface tension. Let us state that as λmin ≈17 mm, at λ < 20 mm the surface tension mechanism has to dominate, and then the increasing wave velocity with surface tension seems natural.
Laboratory workshop in General Physics designed by us [16] for studying in English students of engineering specialties (but not for “Engineering Physics” specialty itself) commonly offered by technical universities includes 20 problems, for which, in particular, are equipped laboratories of the Georgian Technical University (Tbilisi, Georgia). Currently, the water surface wave problem is not among them and we have decided to develop it.
The ripple tank Complete 11260-88 produced by PHYWE Systeme GmbH & Co. KG, Gottingen, Germany (Figure 2) serves for the generation and experimental study of 5 – 60 Hz surface waves in water [17]. The integration in the ripple tank generator can cause a plug-shaped exciter to be dipped into the water for the generation of circular surface waves (see the Figure inserted for the scheme in the laboratory work report example).
Plastic foam is stuck to the inner sides of the water filled-in wave tray. This allows an almost complete absorption of the water waves generated in the tray that hit its sides and thereby avoids unwanted interference with wave reflections. Water maximal depth in the tank is about 300 mm, i.e. significantly exceeds group wavelengths of about 10 mm typically observed in that tank. Thus, the surface waves generated in the ripple tank should be considered as deep-water ones.
A light emitting diode (LED), which can be considered as a point source of light, fixed to the bottom of the tank housing illuminates the wave tray from below and produces a representation of the water waves that is rich in contrast. When the drawing table, i.e. screen is placed on the ripple tank, and a sheet of white paper is placed on the table, the water waves can be observed on the sheet of paper. Light from a point source passes through the wave tray and is partially subject to deflection according to the structure of the surface waves. This deflection generates an alternating bright/dark pattern on the screen. As wave troughs make the light divergent and crests – convergent, they can be recognized, respectively, as dark and bright stripes on the observation surface.
In this ripple tank, either continuous or stroboscopic light can be used. Stroboscopic light allows the propagation velocity of the water waves to be slowed down to a complete standstill. The point is that for continuous light, the human eye is only capable of recognizing the wave image in the lower frequency range. Stroboscopic light should be used with shorter wavelengths – higher frequencies, so that wave propagation is slowed down and made visible to the human eye.
Note that a good contrast is only given at small wave amplitudes. At large amplitudes, the emitted light rays combine far before they reach the screen and diverge again on the long way to it. The result is the disappearance of the wave image. For this reason, the optimal generator amplitude should be set for each experiment.
A number of wave phenomena can be observed with an above-described ripple tank. These are generation, propagation, reflection, dispersion, refraction, interference, diffraction, Doppler effect, etc. However, the listed are only observations, not measurements. Here we propose a way, in which the same experimental setup can be directly used to measure the group velocity of surface waves on water.
However, the use of this device for quantitative measurements requires a preliminary determination of its magnification. Let us solve this problem based on the laws of geometric optics (Figure 3). The light source is considered as a point one and the following values are introduced. Let d be the distance from the source to the water surface in the tank, and d' be the distance to the screen. If we assume that the point light source is located at the bottom of the tank, then the distance d is nothing more than the depth of the water. Obviously, their difference
(14)
coincides with the distance between the water surface and the screen plane. Let us denote by r and r’ the radii of the circle of a certain fixed phase of the water surface wave and its image on the screen. From the similarity of the two triangles shown in the Figure 3, it follows the equality of the ratios of their sides:
(15)
From this, we get the expression for magnification:
(16)
According to our estimates based on the relative positions of the point light source, water surface, and screen in the ripple tank, image magnification should be approximately 1.36.
Let Λ* is the measured on the screen, i.e., apparent group wavelength, then the true group wavelength and group velocity are
(17)
and
V = Λf (18)
respectively.
An example of the proposed laboratory work report is presented below. It is prepared according to the laboratory works report template used in the Georgian Technical University (Tbilisi, Georgia). Template includes the following sections: Scheme (here Figure 4 shows the circular waves on the water surface in used ripple tank), Basic Formulas, Table (here Table 1 represents the results of measurement of group velocity of surface waves in water in dependence of group wavelength), Calculations, Curve (here Figure 5 shows the group velocity of surface waves on water in dependence on group wavelength both as experimental points and theoretical curve), and Brief Description of Problem Execution.
| Table 1: Results of measurement of group velocity of surface waves in water in dependence of group wavelength. | ||||||||||
| # | Frequency f, Hz | Apparent group wavelength Λ*, mm |
Image magnification Γ | Group wavelength Λ, mm | Experimental group Velocity Vexp, mm/s |
Acceleration of gravity g , m2/s |
Water density ρ, kg/m3 | Water–air interface tension coefficient σ, N/m |
Theoretical group velocity Vtheo, mm/s |
Relative error δV, % |
| 1 2 3 4 |
60 50 40 30 |
8.6 10.0 11.9 13.2 |
1.36 | 6.3 7.4 8.8 9.7 |
379 368 350 291 |
9.81 | 1000 | 0.0727 | 395 365 332 313 |
4.1 0.0 5.4 7.0 |
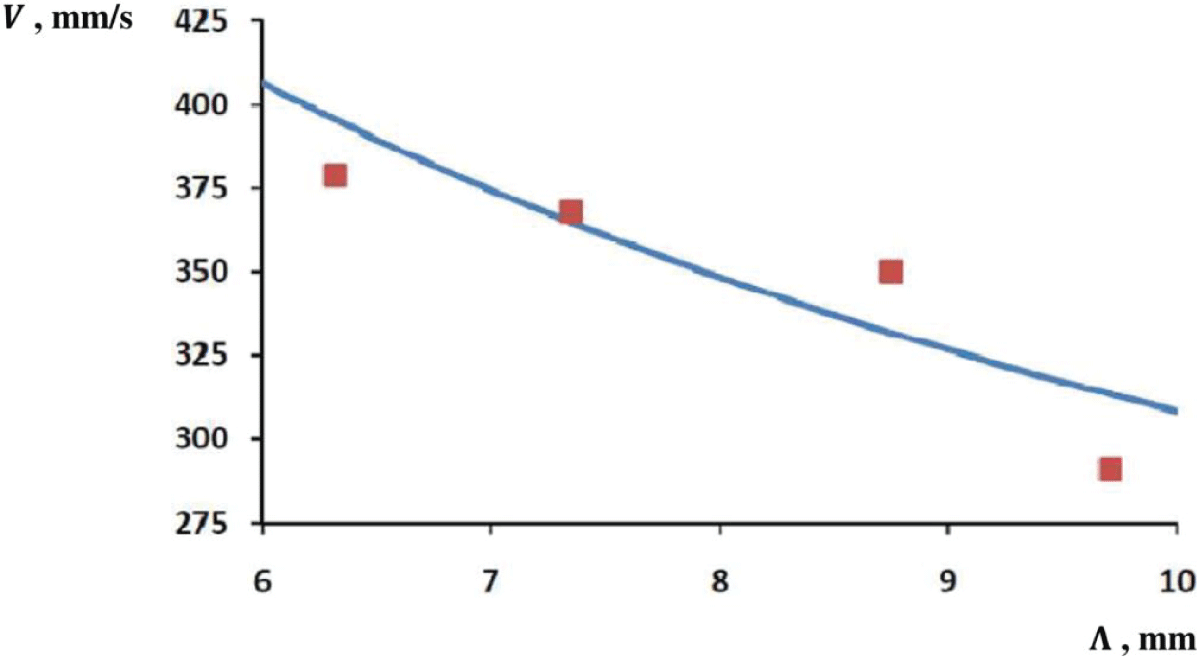 Figure 5: Group velocity of surface waves on water in dependence on group wavelength: experimental points and theoretical curve.
Figure 5: Group velocity of surface waves on water in dependence on group wavelength: experimental points and theoretical curve.Report
Laboratory Work No: [ number ]
Problem No: [ number ]
Title of Problem: Determination of Group Velocity of Surface Waves on Water
Faculty: Faculty of Informatics and Control Systems (Georgian Technical University)
Course: General Physics – 1
Group: [ number ]
Student: [ Name Surname ]
Scheme
Basic formulas
Vexp = Λf
Λ group wavelength
Λ* apparent group wavelength
Λ* magnification
f frequency of wave generator
Vexp experimental group velocity
Vtheo theoretical group velocity
g acceleration of gravity
ρ water density
σ water–air interface tension coefficient
δV relative error
Table
Calculations
Brief Description of Problem Execution
The purpose of the laboratory problem was to determine the group velocity of waves propagating on the water surface. The measurements were carried out on the ripple tank Complete 11260-88. The apparent group wavelength was measured from the image on the screen, and the true group wavelength was recalculated taking into account the setup magnification. Then based on the detected value of the wave generator’s oscillation frequency, the experimental value of surface wave group velocity was determined. For the same group wavelength, the theoretical group velocity was calculated as well. The measurement accuracy was estimated by the relative deviation of the experimental value from the theoretical one. These experiments were repeated at four different frequencies. The experimental group velocities range of 290 – 380 mm/s was found to have corresponded to the frequency range of 30 – 60 Hz. Their average deviation from the theoretically calculated values was found to be about 4%.
Lecturer: [ signature ]
Date: [day/month/year]
The oscillation frequency f in the generated surface waves was detected with an absolute error of about 0.5 Hz, which for the frequency range 30 – 60 Hz of the performed measurements corresponds to a relative error of about 1%. The absolute error in measuring water depth d, distance ∆d between the surface of water and screen, and apparent wavelength Λ* was 0.05 mm, which at the ripple tank’s given dimensions (width × length × height = 300 × 370 × 330 mm) and apparent wavelength of about 10 mm means relative errors of about 1 and 0.5%, respectively, for magnification and apparent wavelength. Summing up these percentages, we obtain about 2.5% for the error in the experimental determination of the group velocity of waves on the water surface. Therefore, the averaged δV deviation of about 4% from theoretical values being quite small itself nevertheless is higher than expected.
In this regard, it should be taken into account that the values of the theoretical curve’s parameters ρ, and σ are known only approximately. In addition, the errors associated with the wave packet model description of the surface wave groups generated in the installation are practically unknown. This is the reason why the relative error in the above laboratory work is estimated as averaged relative deviations of measured values of group velocity from theoretical ones corresponding same group wavelengths.
Here, we aimed to introduce the problem of surface waves on water into the General Physics laboratory workshop. Achieving this aim has been demonstrated by elaborating on the Laboratory Problem: “Determination of Group Velocity of Surface Waves on Water”. Providing explanations of how students can adjust the experimental parameters, such as wave frequency and amplitude, to explore other phenomena related to water surface waves needs further development of corresponding laboratory problems.
It is expedient to compare the obtained here and previously published experimental data on surface waves in water to contextualize the accuracy of the conducted measurements.
In order to observe this interesting phenomenon, Professors of three secondary schools and the City University of Hong Kong built [18] a quite large (6 × 4 × 2 ft) water tank to investigate the relation between wavelength and wave velocity under different water depths. Measured wave velocities agree with the theoretical values when the wavelength is large enough: λ > 20 mm. They have made measurements of the wave velocity for water depths of 25 and 40 mm. In most cases, the uncertainty was about 5%. However, occasionally the uncertainty was up to 15% for waves with highly erratic waveforms.
Our (for a water depth of 300 mm) and part of their results corresponding to the lower wavelength are merged in Table 2. One can state that orders of magnitude of the group velocity measured values, trends of its group wavelength-dependence, and measurement accuracies are the same.
Table 2: Experimental values of group wavelength and corresponding group velocity for surface waves on water of different depths. |
|||
| # | Group wavelength, mm | Group velocity, mm/s | Water depth, mm |
| 1 2 3 4 5 6 7 |
6.3 7.4 8.8 9.7 11.6 15.3 21.4 |
379 368 350 291 258 243 238 |
300 300 300 300 40 40 25 |
Based on the analytical expression for the dispersion relation V = V(Λ) which was obtained theoretically for packets of surface waves in water, the dependence of the propagation velocity V of a group of such waves on its group wavelength Λ has been analyzed. It is concluded that at sufficiently short group wavelengths, the group velocity should rapidly decrease, while at sufficiently long waves, on the contrary, it should increase very slowly. Physically, this behavior of the dispersion function should be associated, respectively, with the dominance of capillary and gravitational mechanisms generating surface waves in water. Between these two limiting cases there is placed a group velocity minimum, Vmin = 163 mm/s, which corresponds to the group wavelength of Λmin = 43.6 mm. The constructed theoretical curve in its general shape is in good agreement with the known experimental curves measured in various water reservoirs and seas.
In order to make a quantitative comparison between theory and experiment, the measurements were carried out in a standard laboratory water tank equipped with a low-frequency generator of circular surface waves. The frequency range of measurements, f = 60 – 30 Hz, approximately corresponds to the range of group wavelengths of Λ = 6 – 10 mm, which is placed on the decreasing branch (Λ/Λmin ≤ 0.23 << 1) of the dispersion function. On average, the experimental values of group velocity deviate from the theoretical ones by 4%.
The used ripple tank serves for measuring the parameters of surface waves in water in the frequency range of 5 – 60 Hz, which corresponds to the group wavelength values of about 10 mm. Figure 1 shows that the experimental study of all the main features of such waves needs generator modification to widen the group wavelengths range to 1 – 100 mm. However, to retain the deep-water approximation accuracy at a surface wavelength of 100 mm, one should increase the water maximal depth in the tank by about 3 times.
Finally, we conclude that the measurements carried out provide acceptable accuracy and confirm the theoretically expected dependence of the group velocity of waves on the water surface on their group wavelength.
Scanlon E, Schreffler J, James W, Vasquez E, Chini JJ. Postsecondary physics curricula and universal design for learning: Planning for diverse learners. Phys Rev Phys Educ Res. 2018;14(2):020101.
Bonacci E. On teaching quantum physics at high school. Athens J Edu. 2020;7(3):313-330.
Atanas JP. Is virtual-physical or physical-virtual manipulatives in physics irrelevant within studio physics environment? Athens J Edu. 2018;5(1):29-42.
Delgado-Cepeda FJ. Widget based learning in math and physics undergraduate courses as blended learning approach. Athens J Edu. 2016;3(3):241-260.
Maschietto M, Turrini M. The laboratory of mathematical machines: Exhibitions, educational research and sessions for students. Educ Res Rev. 2017;7(3):47-52.
Rossi AV. “Talk about chemistry”: A voluntary and effective integration among the players of teaching chemistry. Athens J Edu. 2016;3(3):273-282.
Wartha EJ, Andrade dos Santos CM, Galdino da Silva RA, Mota de Jesus R. The concept of electronegativity: Approximations and separations in chemistry textbooks. Educ Res Rev. 2013;3(2):113-117.
Gyasi H, Ofosu Ofoe E, Bobonkey Samlafo V. The effect of molecular model sets on students’ academic performance in naming organic compounds. Educ Res Rev. 2018;8(3):37-41.
Hansen S. 100 years of the Knudsen gauge. Vac Technol Coat. 2018;19(5):12-16.
Mbonyiryivuze A, Yadav LL, Amadalo MM. Students’ conceptual understanding of electricity and magnetism and its implications: A review. Afr J Educ Stud Math Sci. 2019;15(2):55-67.
Aygun M, Hacioglu Y. Teaching the sound concept: A review of science and physics education postgraduate theses in Turkey. Athens J Edu. 2023;9(2):257-278.
Calalb M. The constructivist principle of learning by being in physics teaching. Athens J Edu. 2023;10(1):139-152.
Mei CC. Waves in water. In: 1.138J/2.062J/18.376J, Wave Propagation. Cambridge (MA): MIT; 2004. p. 40. Available from: http://web.mit.edu/1.138j/www/material/chap-4.pdf
Chikhladze M, Kantaria I, Chkhartishvili L. On group velocity of wave propagation on water surface. Nano Stud. 2017;15/16:53-60.
Baldock TE, Swan C, Taylor PH. A laboratory study of nonlinear surface waves on water. Phil Trans R Soc Lond A. 1996;354(1707):649-676.
Kvintradze V, Chkhartishvili L. Laboratory Workshop in General Physics. Tbilisi: Publishing House “Technical University”; 2020. 136 p.
PHYWE Systeme. Operating Instructions. Ripple Tank with LED Light Source, Complete 11260-88. Gottingen (Germany): PHYWE Systeme GmbH & Co. KG; 2020. 5 p. Available from: www.phywe.com
In LW, Lun LY, Kin LM, Cheung H-F. Surface wave on water. Hong Kong: Physical Society of Hong Kong; 1996. 12 p. Available from: http://www.phys.ust.hk/genphys/press/cityu.pdf
L C, M C, I K. Problem of Surface Waves on Water in Higher School Laboratory Workshop. IgMin Res. October 22, 2024; 2(10): 826-834. IgMin ID: igmin255; DOI:10.61927/igmin255; Available at: igmin.link/p255
Anyone you share the following link with will be able to read this content:
Address Correspondence:
Levan Chkhartishvili, Professor, Engineering Physics Department, Georgian Technical University, 77 Merab Kostava Avenue, Tbilisi, 0160, Georgia, Email: [email protected]
How to cite this article:
L C, M C, I K. Problem of Surface Waves on Water in Higher School Laboratory Workshop. IgMin Res. October 22, 2024; 2(10): 826-834. IgMin ID: igmin255; DOI:10.61927/igmin255; Available at: igmin.link/p255
Copyright: © 2024 Chkhartishvili L, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
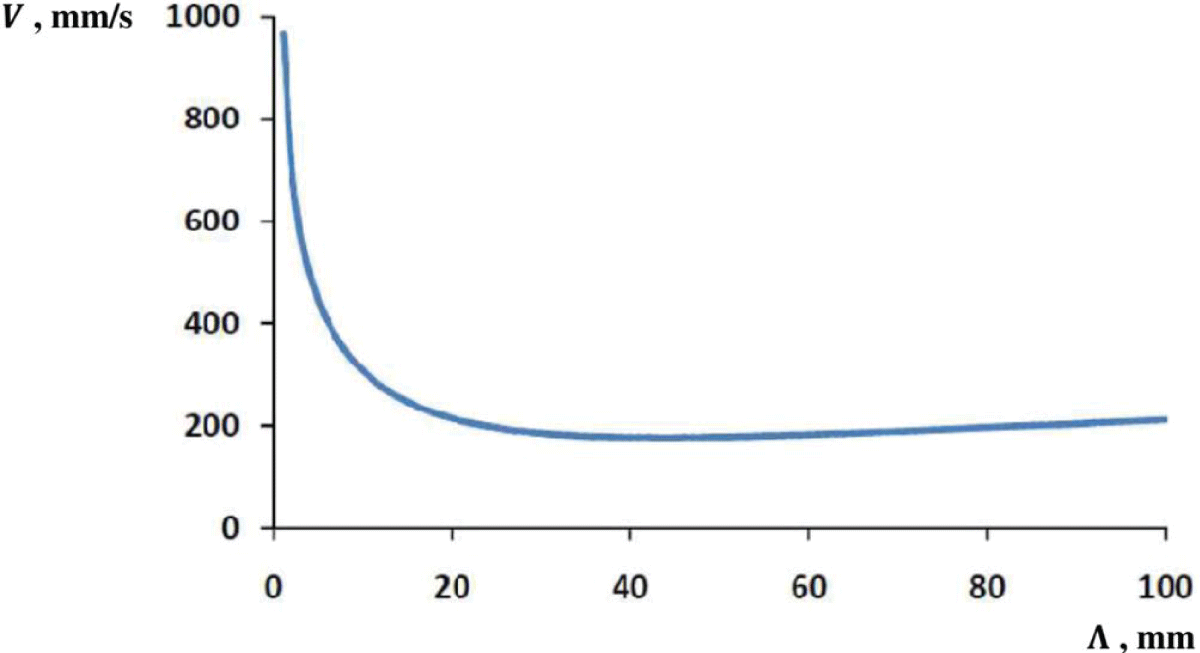 Figure 1: Theoretical dependence of water surface waves grou...
Figure 1: Theoretical dependence of water surface waves grou...
 Figure 2: Ripple tank with light source Complete 11260-88....
Figure 2: Ripple tank with light source Complete 11260-88....
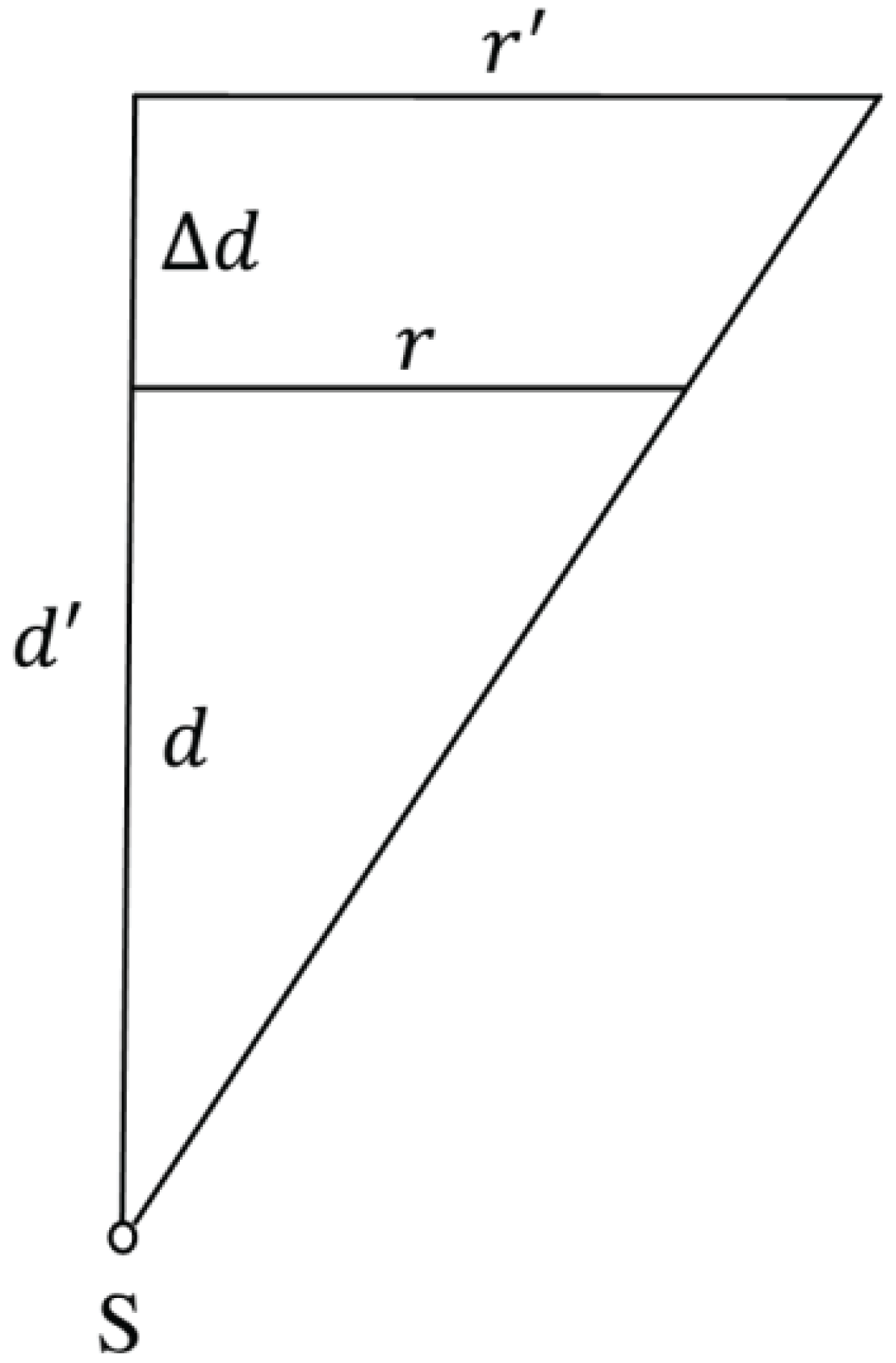 Figure 3: Determination of magnification of ripple tank with...
Figure 3: Determination of magnification of ripple tank with...
 Figure 4: Circular waves on the water surface in the ripple ...
Figure 4: Circular waves on the water surface in the ripple ...
 Figure 5: Group velocity of surface waves on water in depend...
Figure 5: Group velocity of surface waves on water in depend...
Scanlon E, Schreffler J, James W, Vasquez E, Chini JJ. Postsecondary physics curricula and universal design for learning: Planning for diverse learners. Phys Rev Phys Educ Res. 2018;14(2):020101.
Bonacci E. On teaching quantum physics at high school. Athens J Edu. 2020;7(3):313-330.
Atanas JP. Is virtual-physical or physical-virtual manipulatives in physics irrelevant within studio physics environment? Athens J Edu. 2018;5(1):29-42.
Delgado-Cepeda FJ. Widget based learning in math and physics undergraduate courses as blended learning approach. Athens J Edu. 2016;3(3):241-260.
Maschietto M, Turrini M. The laboratory of mathematical machines: Exhibitions, educational research and sessions for students. Educ Res Rev. 2017;7(3):47-52.
Rossi AV. “Talk about chemistry”: A voluntary and effective integration among the players of teaching chemistry. Athens J Edu. 2016;3(3):273-282.
Wartha EJ, Andrade dos Santos CM, Galdino da Silva RA, Mota de Jesus R. The concept of electronegativity: Approximations and separations in chemistry textbooks. Educ Res Rev. 2013;3(2):113-117.
Gyasi H, Ofosu Ofoe E, Bobonkey Samlafo V. The effect of molecular model sets on students’ academic performance in naming organic compounds. Educ Res Rev. 2018;8(3):37-41.
Hansen S. 100 years of the Knudsen gauge. Vac Technol Coat. 2018;19(5):12-16.
Mbonyiryivuze A, Yadav LL, Amadalo MM. Students’ conceptual understanding of electricity and magnetism and its implications: A review. Afr J Educ Stud Math Sci. 2019;15(2):55-67.
Aygun M, Hacioglu Y. Teaching the sound concept: A review of science and physics education postgraduate theses in Turkey. Athens J Edu. 2023;9(2):257-278.
Calalb M. The constructivist principle of learning by being in physics teaching. Athens J Edu. 2023;10(1):139-152.
Mei CC. Waves in water. In: 1.138J/2.062J/18.376J, Wave Propagation. Cambridge (MA): MIT; 2004. p. 40. Available from: http://web.mit.edu/1.138j/www/material/chap-4.pdf
Chikhladze M, Kantaria I, Chkhartishvili L. On group velocity of wave propagation on water surface. Nano Stud. 2017;15/16:53-60.
Baldock TE, Swan C, Taylor PH. A laboratory study of nonlinear surface waves on water. Phil Trans R Soc Lond A. 1996;354(1707):649-676.
Kvintradze V, Chkhartishvili L. Laboratory Workshop in General Physics. Tbilisi: Publishing House “Technical University”; 2020. 136 p.
PHYWE Systeme. Operating Instructions. Ripple Tank with LED Light Source, Complete 11260-88. Gottingen (Germany): PHYWE Systeme GmbH & Co. KG; 2020. 5 p. Available from: www.phywe.com
In LW, Lun LY, Kin LM, Cheung H-F. Surface wave on water. Hong Kong: Physical Society of Hong Kong; 1996. 12 p. Available from: http://www.phys.ust.hk/genphys/press/cityu.pdf