
Properties of Indium Antimonide Nanocrystals as Nanoelectronic Elements
ElectronicsReceived 04 Dec 2023 Accepted 29 Dec 2023 Published online 30 Dec 2023
ISSN: 2995-8067 | Quick Google Scholar
Next Full Text
Revolutionizing Duplicate Question Detection: A Deep Learning Approach for Stack Overflow


Received 04 Dec 2023 Accepted 29 Dec 2023 Published online 30 Dec 2023
By measurements on single nanocrystals of indium antimonide in the interelectrode nanogap of a scanning probe microscope, current-voltage characteristics with quasiperiodic current pulsations, are explained in the model of Bloch oscillations in a perfect nanocrystal, and individual sharp peaks - conductivity resonances, explained in the model of quantum-size limitation of the wave process of electron transport in a deep potential hole. The mutual influence of radiation from two statistical ensembles of nanocrystals from the same batch was experimentally studied and established. It is assumed that this radiation is entangled photons. It is proposed to use nanocrystals in nanoelectronics as a single-electron memristor, a single-photon bolometer, and a source of microwave radiation.
The most studied objects in the areas of nanotechnology and nanoscience are nanoparticles, with their characteristic sizes less than 100 nm, and, in particular, quantum dots (QD), which are understood not only as zero-dimensional formations, in their true physical meaning, but also, in general, any nanoparticles with sizes less than 10 nm [-]. (In our opinion, it is more correct to apply to them the term “quantum-sized particle” (QP), which we first used in []). The fundamental distinguishing property of QD and QP is size quantization, which manifests itself in the properties of the band structure as the dependence of electron energy on size. This manifestation is most simply observed in optical properties directly related to the properties of the band structure, the study of which is the subject of most studies. In this case, a model of dimensional limitation of exciton motion is used. However, as shown in our work [], the size limitation of the motion of an electron and an exciton are competing processes when, for example, photoluminescence is worse, the better the size quantization parameters of the QD. The physical reason for this is the rapid decay of the exciton due to the predominance of the motion of the “light” electron over its Coulomb approach to the hole. Fundamental manifestations of size quantization in a quantum-sized nanoparticle are associated with its conductivity. In a quantum dot, as a quasi-zero-dimensional formation, the conductivity is determined by the recharging of the nanocapacitor and the ballistic jump of the electron, which was first studied theoretically and experimentally by Nobel laureate A.I. Ekimov. With collaborators in works that have become classics []. At the same time, specific manifestations were discovered - the Coulomb blockade and Coulomb “ladder”. This model is used in theoretical calculations and assessments of real structures with reduced dimensionality []. A quantum-sized particle, in fact, is not a zero-dimensional formation, having the properties of an extended potential well. Its conductivity is more complex, determined by several physical processes []. This issue has been considered theoretically in a number of works [,]. Studies of electron transport in semiconductor nanoparticles mainly concern their arrays [-]. Reports of experimental studies of electron transport in individual semiconductor nanoparticles are extremely rare. In [], such a study was carried out on individual quantum dots of PbS nanocrystals using scanning probe microscopy using one or two monolayer films of nanocrystals.
We have studied options for step-by-step single-electron transport - emission-injection penetration of an electron into a quantum-sized particle and tunneling from it, a specific process of its movement in it, like an extended potential well [,,]. We consider the movement of an electron inside a QP as a wave oscillatory process between its boundaries, including several specific variants - quantum resonance, Bloch oscillations, and Coulomb limitation. This movement inside occurs until a probabilistic tunnel transition occurs into the nanogap between the nanoparticle and the electrode. We call the quantum resonant motion of an electron quantum conductivity with its description by the quantum thread model []. The quantum-dimensional nature of conductivity implies the passage of physical processes in the crystal structure of a nanoparticle, which is actually a perfect nanocrystal (NC). The term “nanocrystal” appeared, apparently, immediately after the word “nanotechnology” was first named and published (N. Taniguchi, 1974). However, it began to be widely used in the literature not so long ago, when research began on semiconductor nanoparticles of various shapes. Several reviews are devoted to the topic of nanocrystals, for example, []. The production and study of semiconductor nanocrystals is currently an important scientific and technical problem.
In recent years, there has been increased interest in one of the phenomena predicted by the theory - quantum entanglement. The Nobel Prize was awarded in 2022 for experiments with entangled photons. We attempted a similar experiment on indium antimonide quantum dots, as reported in our work [].
The importance of this research work is due to the relevance of solving issues of determining the properties of semiconductor nanocrystals, which can be elements of nanoelectronics, in particular, for supercomputers and photonic computers. It should be noted that on application issues, most works are devoted to the optical properties and photoluminescence in quantum dots. Applications in nanoelectronics are still in the stages of fundamental research.
The novelty of this research work is that studies of the properties of single semiconductor nanocrystals are extremely rare in the literature. This especially applies to the properties of quantum conductivity and photonic entanglement in nanocrystals.
This paper presents the results of our continued research in the areas of possible manifestations of quantum conductivity and photonic entanglement in the most interesting object for this purpose - quantum-sized nanoparticles of indium antimonide, which have the best size quantization parameters of all semiconductors. NC-InSb nanocrystals were produced by colloidal synthesis and had sizes in the range of 3 – 7 nm with an approximately Gaussian distribution with a maximum of 5 nm. The technology and control of properties are described in our work []. Measurements of current-voltage characteristics (CVC) were carried out on scanning probe microscopes SOLVERNano (120 nA/5V) and NANOEDUCATOR (50 nA/2V) in the field emission mode from a probe with a gap of ~5 nm using the methods described in our work [].
Thus, in contrast to works known from the literature, in our present work, important new physical phenomena of quantum conductivity and oscillations, expressed in the form of quasiperiodic oscillations and resonant current peaks in the current-voltage characteristics, were experimentally studied on single nanocrystals. The manifestations are explained in models of Bloch oscillations and de Broglie waves in a nanocrystal as a deep, extended quantum well.
Figure 1a shows typical current-voltage characteristics for NC-InSb, which have features in the form of individual sharp peaks and quasi-periodic current pulsations (curves 1, 2). CVC cr. 1* has the least manifestations of features. Curves 3 and 4 are test ones, showing the absence of observable features for simple options - InSb submicroparticles and contact of the probe with the ITO electrode. We explain the differences in the types of current-voltage characteristics (Figure 1a) by the degree of manifestation of size quantization.
 Figure 1: a: Current-voltage characteristic: 1.1*.2 – NC-InSb; 3 – submicro-InSb test; 4 – ITO test; b – Conductivity peaks, numbers above the curves – calculated values of dimensions an for cases k = 1 (single and bottom) and k = 2 (top)
Figure 1: a: Current-voltage characteristic: 1.1*.2 – NC-InSb; 3 – submicro-InSb test; 4 – ITO test; b – Conductivity peaks, numbers above the curves – calculated values of dimensions an for cases k = 1 (single and bottom) and k = 2 (top)The current-voltage characteristics of nanocrystals (NC) with a weak manifestation of size quantization (curve 1*, Figure 1a) have regions limited by the processes of tunneling overcoming barriers during the injection of an electron into the nanocrystal and its emission from it [,]. Electron transport inside a nanocrystal occurs by its field drift. Under the influence of an external constant field in a nanocrystal, an electron in the space of the band diagram E(k) makes a jump-like motion (Bloch oscillations) along the kx axis near the origin of coordinates in the scheme of reduced repeating Brillouin zones and oscillates on a limited segment of the x axis along the field Fx with an amplitude ax ~ Eg (2qFx)-1 (q is the electron charge, Eg is the band gap of the semiconductor nanocrystal) [].
If we assume that ax is equal to the nanocrystal lattice constant a0, and the field is Fx ~ V/an, (V is the potential difference across the NC, an is the nanocrystal size), then we can estimate the quasi-period of voltage oscillations on the current-voltage characteristic – q∆V~Eg/2, for NC-InSb – 0.08 eV. An estimate from experiments (such as Figure 1a) gave values of ~ (0.08 ± 0.02) eV. It is necessary, however, to note that Bloch oscillations practically do not appear in bulk crystals due to the scattering effect of defects and thermal vibrations of the lattice. However, in nanocrystals, due to their high structural perfection in an extremely small volume, Bloch oscillations can be observed experimentally, just as, for example, in superlattices []. The manifestation of Bloch oscillations, thus, characterizes the structural perfection of NC-InSb and, in connection with this, the possibility of quantum conductivity.
The movement of an electron through a nanocrystal is described by the solution of the Schrödinger equation and the de Broglie wave process. In the simple case of a one-dimensional one-electron process in a deep rectangular extended potential well at a linear distance of one of the nanocrystal sizes an, the values of the allowed electron energy levels Ẽkn and the probability K* of electron passage through the nanocrystal, as an extended potential barrier, can be obtained in the following form []:
Ẽkn ~ h2k2(8man2)–1 ~ 0.37k2(m/m0)–1an–2, (1)
K*~ exp[–4πan(2mẼkin)1/2/h] ~ exp[–4V *], (2)
Where: Ẽkin ~ (Ẽkn – qV) – kinetic energy of the electron; V* ~ (k2 – 2.7Van2m/m0)1/2 – dimensionless parameter depending on voltage V – potential difference (voltage drop) across NC; h – Planck’s constant; k – quantum number; m is the effective mass of an electron in a nanocrystal semiconductor; m0 – mass of a “free” electron; Ẽkin, Ẽkn – in electronvolts, an – in nanometers.
The formula for the current-voltage characteristic, when the current is limited by the probability of an electron passing through a nanocrystal, can be written based on formula (2) in the following form:
I ∝ K* ~ exp[–4V*] ~ I0exp[–4V*] (3)
Conductivity G can be estimated by differentiating the current-voltage characteristic of formula (3):
G ~ dI/dV ~ –4I(dV*/dV) ~ 5.4(I/V*)an2m/m0 (4)
As follows from formula (4), the condition for conductivity resonance will be V* ~ 0.
Figure 1b shows typical characteristics of differentiation of the current-voltage characteristics and, accordingly, conductivity peaks dI/dV = G in the observation zones of resonant current peaks. The numbers on top of the peak curves indicate the sizes an, calculated from the resonance condition k2 ~ 2.7Van2m/m0. These values correlate satisfactorily with the data of actually measured sizes, taking into account the actions of resonant modes of the 1st and 2nd orders.
Experimental values of G fluctuate in the range (1 ÷ 2)•10–6 S (Figure 1b). These data can be compared with theory by calculating the values of G using the formula (4). The calculation showed that the G values are approximately an order of magnitude lower than those measured experimentally. In this regard, we proposed to use the quantum thread model []. In this model, taking into account the single-electron nature of the current, G ~ K–1q2/h ~ 4•10–5K–1 S, where: q is the electron charge, K is the number of quantum steps. The ratio an/a0 can be taken as the number K. In our case, an/a0 ~10. Then: G ~ (1 ÷ 4)•10–6 S, which corresponds to experiment.
A deep, extended one-dimensional potential well of a quantum-sized particle can be considered as a single-electron nanoresonator, to which two physical models are applicable: a quantum oscillator and an electrodynamic generator. In the electrodynamic model: an electron accelerates in the field of a nanocrystal, increasing its energy, then is reflected from the boundary of the nanocrystal and then flies in a decelerating field, releasing energy in the form of electromagnetic radiation (EMR). When exposed to external EMR, the nonequilibrium quasi-free electron is heated by the electric field of the wave []. In this case, the field value, estimated in our case, at a minimum, as (104 ÷ 105) V/cm, is one to two orders of magnitude higher than the values of the minimum limit of the heating effect calculated in [].
In the quantum oscillator model, the radiation frequency is ν ~ Ẽkn/h ~ 5•1012 Hz – under the conditions an = 5 nm and m/m0 = 1 (under quantum resonance conditions). The time of the electron transport period calculated from the values of the single-electron current is (2÷5)•10-12 s. The radiation frequency is ~(0.2 ÷ 0.5)•1012 Hz, which, in fact, must be multiplied by the number of oscillations during the flight of the electron.
It seems to us that, due to the resonant state of motion of a single electron in a nanocrystal, the radiation should be strictly parameterized and interact only with a medium similar to the one that produced it. We would call the photons carrying this radiation and the information “hardwired” in it wandering, believing that they can be likened to entangled photons. In this case, the interaction of two identical samples should appear, located at some distance from each other and devoid of any interaction of an obvious nature - electric and electromagnetic-wave.
We carried out such an experiment on two identical NANOEDU-CATOR scanning probe microscopes. First, the current-voltage characteristics of each sample were measured when switched on separately, and then when switched on simultaneously. On each of the samples, 25-30 points (NC) were selected in the same zone, the current-voltage characteristics were measured and statistical analysis was carried out. Figure 2 shows typical current-voltage characteristics of NC-InSb samples without interaction (curves 1 and 2) and with their interaction with supposed radiation (curves 1* and 2*). The current-voltage characteristics with the manifestation of resonance (characteristic resonance peaks) are significantly relatively shifted (Figure 2a). The current-voltage characteristics without them did not change qualitatively (Figure 2b).
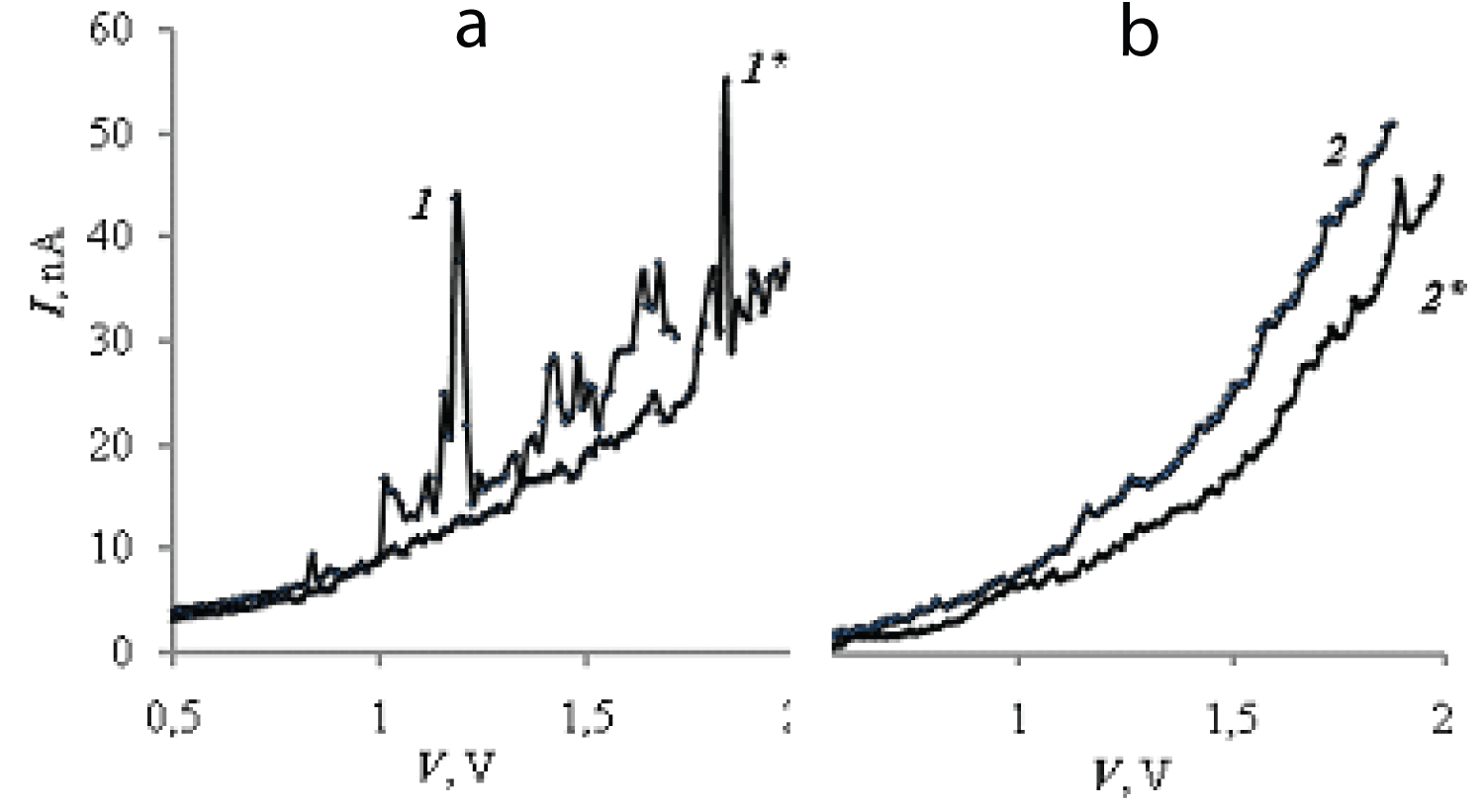 Figure 2: Typical current-voltage characteristics of QP-InSb samples without interaction (1 and 2) and with interaction with supposed radiation (1* and 2*). a – current-voltage characteristics with characteristic resonant peaks; b – without them.
Figure 2: Typical current-voltage characteristics of QP-InSb samples without interaction (1 and 2) and with interaction with supposed radiation (1* and 2*). a – current-voltage characteristics with characteristic resonant peaks; b – without them.Table 1 shows statistical data on changes in the current-voltage characteristics, from which it follows that the positions of the peaks (voltage values) have significantly shifted towards larger values. At the same time, for the same reason and taking into account the limited voltage range (no more than 2 V), the proportion of the current-voltage characteristic without peaks has increased significantly.
 Table 1: Data on changes in the current-voltage characteristics of remotely interacting nanocrystals.
Table 1: Data on changes in the current-voltage characteristics of remotely interacting nanocrystals.We explain the observed phenomenon by the fact that in the range of nanocrystals of the same batch, there will always be absolutely identical in shape and size emitting absolutely identical photons at the same time, which may be equivalent to the phenomenon of entanglement.
Thus, the results of studying the current-voltage characteristics of InSb nanocrystals suggest that they can exhibit the phenomena of quantum conductivity and mutual influence of parameterized radiation of photons that are absolutely identical, generated by identical single nanocrystals, which, in this regard, can be considered similar to entangled photons.
In recent years, many publications have appeared on entangled photons, methods, and devices for their production, for example, [-]. Typically, interacting pairs of photons are produced from laser radiation of super-short (single-photon) duration. Our research leads us to the conclusion that nanocrystals, under certain conditions, can be sources of photons with properties similar to entangled photons
The phenomenon of entanglement is inherent in the states of an electron, transmitted in the properties of the photons emitted by it. An electron, as a quantum mechanical particle, is constantly in motion and emits photons depending on how it moves. In the crystal structure of a quantum-sized nanocrystal, an electron moves resonantly, exhibiting the properties of a quantum oscillator and emitting parameterized microwave radiation. Moreover, its movement spatially (structurally, geometrically) is complex and, therefore, confusing.
Figure 3 fragmentarily displays some possible options for the movement of an electron in a quantum-sized nanocrystal. Being in a nanocrystal, an electron, in the quantum particle model, moves between its boundaries along atomic orbitals, shown in Figure 3 by large circles. In these orbitals, it is quasi-free and has spin. Possible options for its movement are A-B-C, A-D-C, and some other, more complex ones. In addition, the plane of motion can change its angle. All this determines the uncertainty (confusion, entanglement) of the states during the movement of the electron. However, the resonant nature of the movement will determine the choice of its path in favor of the curve that is minimal in size. That is, we can assume that it will move along the A-B-C curve.
The resonant nature of electron motion in a nanocrystal is due to the de Broglie wave process and reflections of waves from crystallographic planes and boundaries of the nanocrystal. The transport process is single-electron with manifestations of quantum conductivity and oscillations, and electron-photon interaction and generation are single-photon.
At certain sections of this movement, the electron experiences inhibition (points O1 and O2), emitting a photon with certain specific properties of an electromagnetic wave. The physical essence of the phenomenon, in our opinion, in this case, is that an electron in a nanocrystal, oscillating resonantly in time and space, creates single-photon (more precisely, photon) radiation with strictly fixed parameters (frequency, polarization, coherence, phase relationships and perhaps something else). Such radiation most likely interacts only with an electron in the same state as the one that emitted it, that is, with exactly the same nanocrystal. In this case, the uncertainty will be expressed in the statistical difference between the technologically specified properties of the nanocrystal and the quantum mechanical states of the electron in it. If it is possible to find two absolutely identical nanocrystals, then only statistically on a large number of nanocrystals of a random sample. In this case, the interaction of two identical samples located at some distance from each other should appear.
In fact, in our case, perhaps this manifestation is not quantum mechanical entanglement. But thanks to tightly parameterized single-photon radiation, which interacts only with its “native” environment, it is possible that its manifestation is similar to quantum entanglement. What we call hard parameterization can be explained as follows.
An incandescent light bulb emits “chaotic” light, which can be characterized by two parameters - power and energy. The emission of an LED can also be characterized by its wavelength. Laser radiation - coherence, monochromaticity, polarization, etc. Single-photon radiation of a nanocrystal has all of the listed parameters and, in addition to them, perhaps some others. We need to look at Figure 3 and imagine the state of the electron at the bifurcation points O1 and O2, in which for an instant (almost zero time interval) the speed is apparently equal to zero, the spin is probably also equal to zero, the field vector abruptly changes direction, well, and so on - something else. In the quantum mechanical model, this phenomenon is caused by the interaction of the de Broglie wave with the atomic plane. The time interval of photon action, in this case, can be estimated at 10–14 ÷ 10–12 seconds, that is, the interval for which quantum entanglement researchers “fight” in experiments with photons of laser radiation.
This simplified consideration leads to the idea that we may be talking about a new type of radiation – single-photon superparameterized radiation from a quantum-sized medium. It can well be defined by the term “superlight”. Its main property is that it does not interact (is not absorbed) with any medium other than the quantum-sized one, which, among other things, has bifurcation electronic states.
The basis of the element base for nanoelectronics is a single-electron transistor, in which noticeable changes in potentials are obtained by manipulating single electrons. Another promising element is a memristor - an electronic component that maintains internal non-volatile resistance for a long time after the external electric field is removed.
Our version proposes a conducting nanocell with quantum-sized particles, which can be an element of a single-electron transistor, memristor, or single-photon pair. A conductive nanocell consists of 2, 3, or 4 electrodes in the form of converging strips of film metal of nano-sized widths and gaps between them []. Such a nanocell can become the basis for the formation of a nanocircuit chip based on the single-electron and single-photon principles. In this case, the following nanoelements will be workers in the nanocircuit.
The memory element is an electronic memristor: Theoretically, a memristor was proposed in 1971 []. The memristor effect consists of changing the resistance of the element under the influence of voltage and maintaining it after its removal []. Methodological foundations for the use of memristors in microelectronics have been created.
According to the current state of technological work in this direction, nano-sized oxide materials are used, which change their structure and, accordingly, resistance under the influence of voltage. It is clear that with this method the performance of the element will not be high. A semiconductor nanocrystal (NC) in its initial state does not conduct and becomes conductive if an electron is injected into it, which, however, under the influence of a field, tunnels out of it after some ultrashort time of its resonant movement into the NC. If this time limits the influence of voltage, then the electron will remain in NC as in a deep, extended potential well. The nanocrystal will be charged with an electron, and this state will remain until a voltage pulse of longer duration than during recording is applied. Such a memristor can be called electronic.
The optocoupler elements are a single-photon emitter and a recorder: As follows from the above data, charge oscillations occur in a quantum-sized nanocrystal due to the resonant motion of an injected electron. In this case, such a quantum oscillator emits photons in the far-infrared and terahertz spectra. In the same nanocrystal, under the influence of radiation, electronic “heating” occurs, causing a change in the position of the resonant peak on the current-voltage characteristic. The effect manifests itself as a photon bolometer. In addition to the ultra-high (picosecond) speed, the radiation of such an optocoupler is parameterized, and it can be expected that it will not respond to external influences, which is important for protection against parasitic influences.
The purpose of the work is to study the properties of indium antimonide nanocrystals as elements of nanoelectronics.
Electron transport in an indium antimonide nanocrystal, manifested by individual resonant current peaks in the current-voltage characteristic, is caused by the de Broglie wave process of electron motion in the nanocrystal as a deep, extended potential well. The resulting quantitative relationships are explained in the quantum thread model.
Quasiperiodic current oscillations are explained in the model of Bloch oscillations, the manifestation of which is due to the high perfection of the nanocrystal and the absence of the influence of phonons in the three-dimensional quantum-size nanostructure. The probabilistic fraction of the number of samples with well-defined current ripples ranged from 15% to 65%, depending on the semiconductor used and the size of the nanocrystals. Moreover, the higher the size quantization parameter, calculated using a formula similar to the expression for the de Broglie wavelength, the greater it is.
One of the important conditions for the use of nanocrystals is the creation of a conducting nanocell with one or more nanocrystals placed between its electrodes. Such a nanocell can become the basis for the formation of a nanocircuit chip based on single-electron and single-photon principles. In this case, the workers in the nanocircuit will be an electronic memristor, a nano-optocoupler made of emitting and recording nanocrystals.
The author is grateful to graduate student M.V. Gavrikov. For SPM measurements of current-voltage characteristics.
Van Embden J, Gross S, Kittilstved KR, Della Gaspera E. Colloidal Approaches to Zinc Oxide Nanocrystals. Chem Rev. 2023 Jan 11;123(1):271-326. doi: 10.1021/acs.chemrev.2c00456. Epub 2022 Dec 23. PMID: 36563316.
Montanarella F, Kovalenko MV. Three Millennia of Nanocrystals. ACS Nano. 2022 Apr 26;16(4):5085-5102. doi: 10.1021/acsnano.1c11159. Epub 2022 Mar 24. PMID: 35325541; PMCID: PMC9046976.
Porotnikov D, Zamkov M. Progress and Prospects of Solution-Processed Two-Dimensional Semiconductor Nanocrystals. The Journal of Physical Chemistry C.2020; 124 (40): 21895-21908. https:/ /doi.org/10.1021/acs.jpcc.0c06868
Alizadeh-Ghodsi M, Pourhassan-Moghaddam M, Zavari-Nematabad A, Walker B, Annabi N, Akbarzadeh A. State-of-the-Art and Trends in Synthesis, Properties, and Application of Quantum Dots-Based Nanomaterials. Part Part Syst Charact. 2019; 36: 1800302. DOI: 10.1002/ppsc.201800302.
Zhukov ND, Sergeev SA, Hazanov AA, IT // Technical Physics Letters. 2022; 48:70-73.
Yekimov AI, Onushchenko AA. Pis'ma v ZHETF. 1984; 40(8): 337.
Dragunov VP, Neizvestnyy IG, Gridchin VA. Fundamentals of Nanoelectronics. M: Logos. 2006.
Zhukov ND, Gavrikov MV. Technical Physics Letters. 2022; 48: 61-65.
Radantsev VF. Electronic properties of semiconductor nanostructures. Ekaterinburg, 2008; 415. https://elar.urfu.ru/bitstream/10995/1473/7/1334870
Lesovik GB, Sadovskiy IA. Scattering matrix approach to the description of quantum electron transport. Advances in physical sciences. 2011; 181(10): 1041.
Glinskiy GF. Pis'ma v ZHTF. 2018; 44(6): 17.
Utsugi T, Kuno T, Lee N, Tsuchiya R, Mine T, Hisamoto D, Saito S, Mizuno H. Phys Rev B. 2023; 108: 235308.
Reich KV. Conductivity of quantum dot arrays. Advances in Physical Sciences. 2020; 190: 1062-1084. DOI: https: //doi.org/10.3367/UFNr.2019.08.038649
Diaconescu B, Padilha LA, Nagpal P, Swartzentruber BS, Klimov VI. Measurement of electronic states of PbS nanocrystal quantum dots using scanning tunneling spectroscopy: the role of parity selection rules in optical absorption. Phys Rev Lett. 2013 Mar 22;110(12):127406. doi: 10.1103/PhysRevLett.110.127406. Epub 2013 Mar 22. PMID: 25166850.
Zhukov ND, Gavrikov MV, Shtykov SN. Dimensional Modeling of the Synthesis and Conductivity of Colloidal Quantum Dots. Semiconductors. 2022; 56: 269-274.
Zhukov ND, Gavrikov MV, Kabanov VF, Yagudin IT. Semiconductors. 2021; 55: 470–475.
Montanarella F, Kovalenko MV. Three Millennia of Nanocrystals. ACS Nano.2022; 16(4):5085-5102. https://doi.org/10.1021/ acsnano.1c11159
Krylsky DV, Zhukov ND. Technical Physics Letters. 2020; 46: 901–904.
Zhukov ND, Gavrikov MV. MNIZH. 2021; 8(110): 19. https://doi.org/10.23670/IRJ.
Dmitriyev IA, Suris RA. Electron localization and bloch oscillations in quantum-dot superlattices under a constant electric field. Physics and Technology of Semiconductors. Physics and Technology of Semiconductors. 2001; 35(2): 219.
Bagrayev NT, Buravlev AD, Klyachkin LYe, Malyarenko AM, Gel'khoff V, Ivanov VK, Shelykh IA. Physics and Technology of Semiconductors. 2002; 36(4): 462.
Vorob'yev LE, Danilov SN, Zerova VL, Firsov DA. Physics and Technology of Semiconductors. 2003; 37(5):604.
Ivashkin A, Abdurashitov D, Baranov A, Guber F , Morozov S, Musin S, Strizhak A, Tkachev I. Testing entanglement of annihilation photons. Scientific Reports. 2023; 13:7559. https://doi.org/10.1038/s41598-023-34767-8
Fujihashi Y, Shimizu R, Ishizaki A. Probing exciton dynamics with spectral selectivity through the use of quantum entangled photons. PhysicalRev Research. 2020; 2: 023256. DOI: 10.1103/PhysRevResearch.2.023256
Lib O, Hasson G, Bromberg Y. Real-time shaping of entangled photons by classical control and feedback. Sci Adv. 2020; 6: eabb62989.
Patent RU 2777199 “Method of manufacturing a conductive nanocell with quantum dots.” Priority 08/10/2021
Chua, Leon O.Memristor-The missing circuit element. IEEE Transactions on Circuit Theory. 1971; 18: 507-519.
Xiao Y, Jiang B, Zhang Z, Ke S, Jin Y, Wen X, Ye Sci Technol Adv Mater. 2023; 24(1): 2162323. doi: 10.1080/14686996.2022.2162323
Zhukov NI. Properties of Indium Antimonide Nanocrystals as Nanoelectronic Elements. IgMin Res. 30 Dec, 2023; 1(2): 175-180. IgMin ID: igmin134; DOI: 10.61927/igmin134; Available at: www.igminresearch.com/articles/pdf/igmin134.pdf
Anyone you share the following link with will be able to read this content:
Address Correspondence:
Nikolai Dmitrievich Zhukov, Limited Liability Company “NPP Volga”, Saratov, Russia, Email: [email protected]
How to cite this article:
Zhukov NI. Properties of Indium Antimonide Nanocrystals as Nanoelectronic Elements. IgMin Res. 30 Dec, 2023; 1(2): 175-180. IgMin ID: igmin134; DOI: 10.61927/igmin134; Available at: www.igminresearch.com/articles/pdf/igmin134.pdf
Copyright: © 2023 Zhukov ND. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
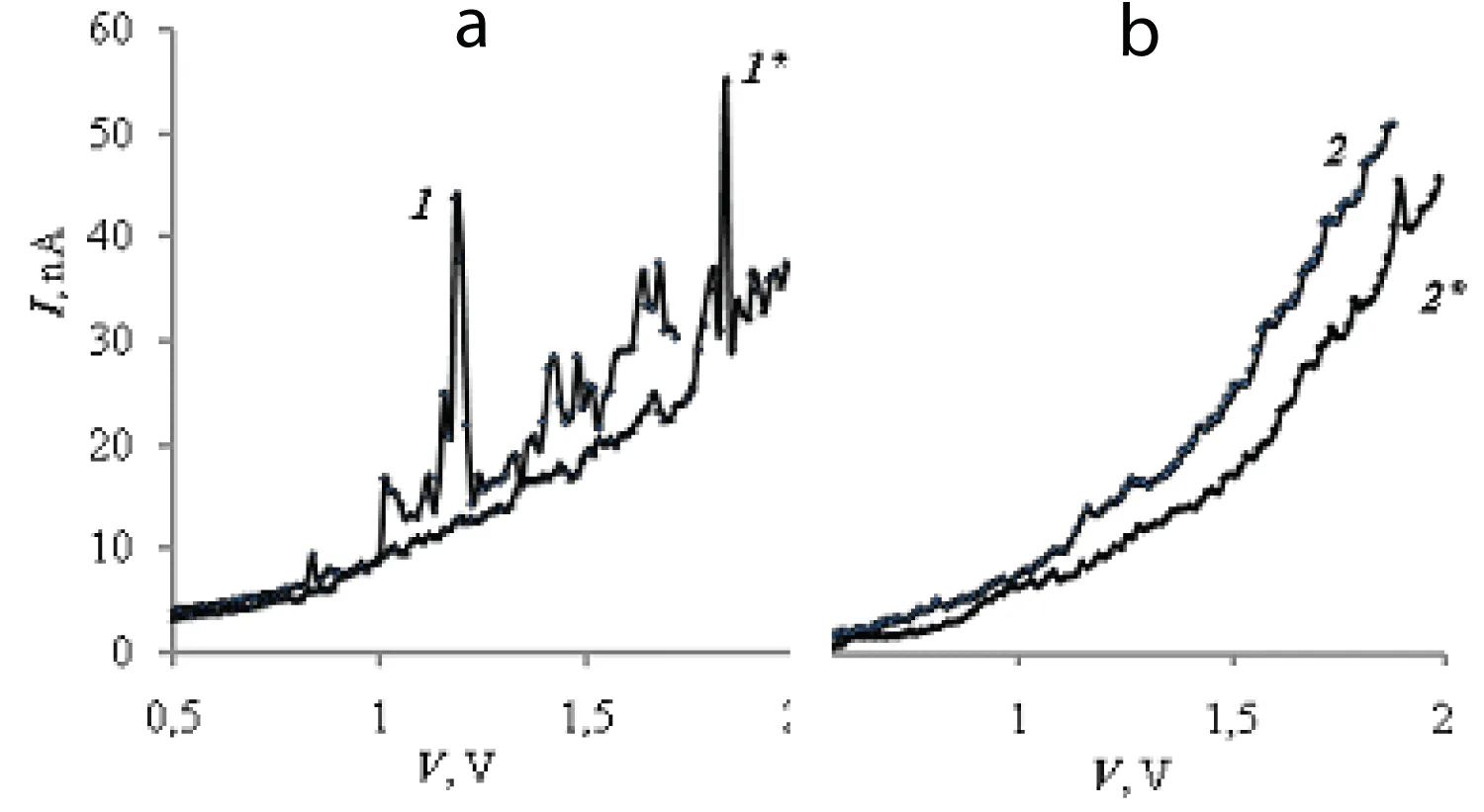 Figure 2: Typical current-voltage characteristics of QP-InSb...
Figure 2: Typical current-voltage characteristics of QP-InSb...
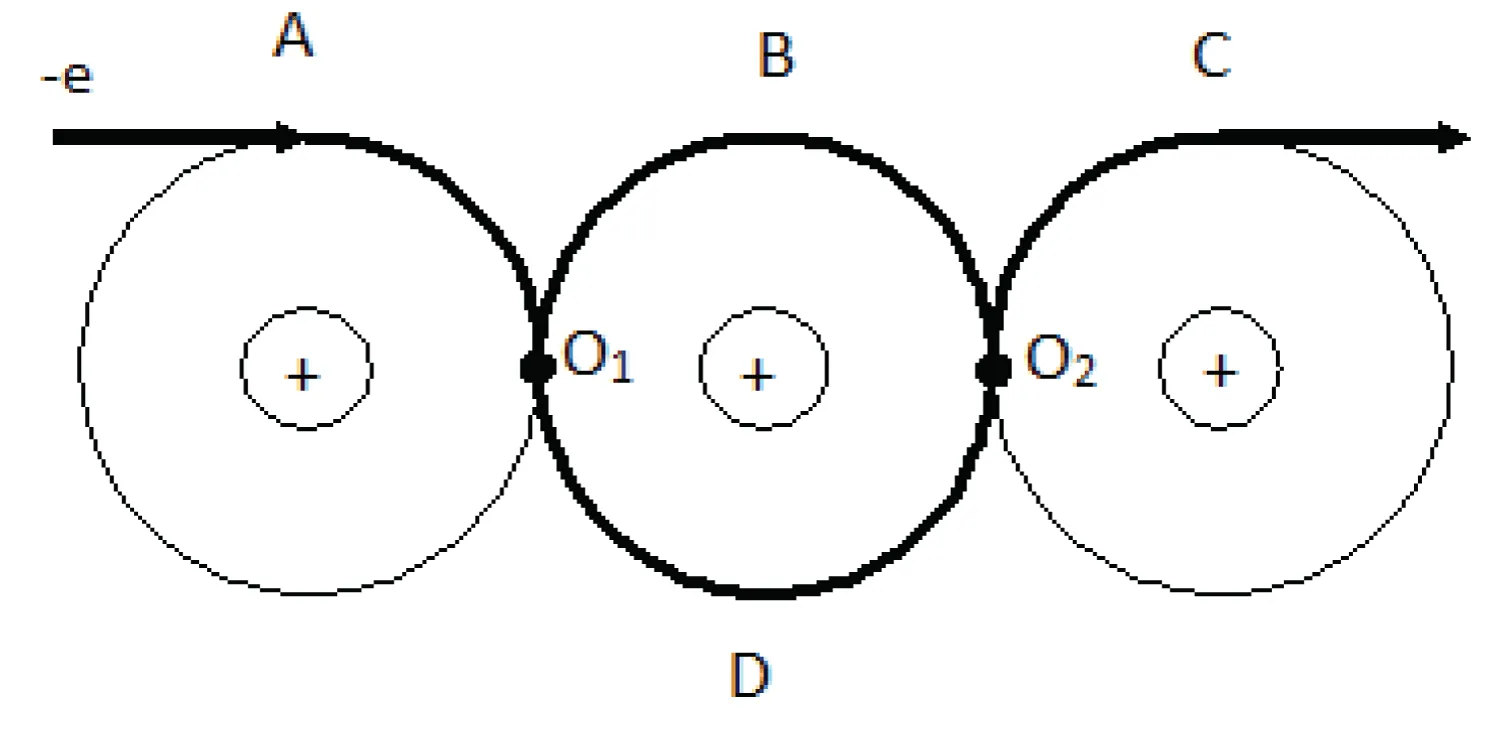 Figure 3: Fragmentary display of electron motion options in ...
Figure 3: Fragmentary display of electron motion options in ...
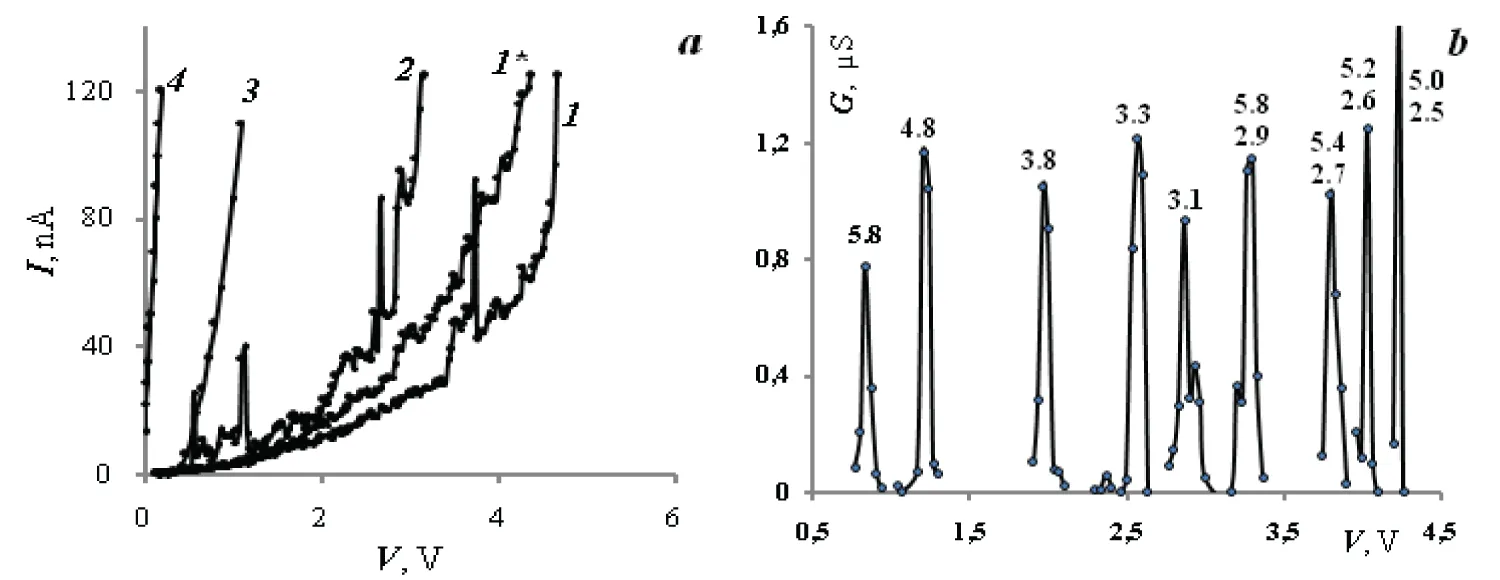 Figure 1: a: Current-voltage characteristic: 1.1*.2 – NC-I...
Figure 1: a: Current-voltage characteristic: 1.1*.2 – NC-I...
 Table 1: Data on changes in the current-voltage characteris...
Table 1: Data on changes in the current-voltage characteris...
Van Embden J, Gross S, Kittilstved KR, Della Gaspera E. Colloidal Approaches to Zinc Oxide Nanocrystals. Chem Rev. 2023 Jan 11;123(1):271-326. doi: 10.1021/acs.chemrev.2c00456. Epub 2022 Dec 23. PMID: 36563316.
Montanarella F, Kovalenko MV. Three Millennia of Nanocrystals. ACS Nano. 2022 Apr 26;16(4):5085-5102. doi: 10.1021/acsnano.1c11159. Epub 2022 Mar 24. PMID: 35325541; PMCID: PMC9046976.
Porotnikov D, Zamkov M. Progress and Prospects of Solution-Processed Two-Dimensional Semiconductor Nanocrystals. The Journal of Physical Chemistry C.2020; 124 (40): 21895-21908. https:/ /doi.org/10.1021/acs.jpcc.0c06868
Alizadeh-Ghodsi M, Pourhassan-Moghaddam M, Zavari-Nematabad A, Walker B, Annabi N, Akbarzadeh A. State-of-the-Art and Trends in Synthesis, Properties, and Application of Quantum Dots-Based Nanomaterials. Part Part Syst Charact. 2019; 36: 1800302. DOI: 10.1002/ppsc.201800302.
Zhukov ND, Sergeev SA, Hazanov AA, IT // Technical Physics Letters. 2022; 48:70-73.
Yekimov AI, Onushchenko AA. Pis'ma v ZHETF. 1984; 40(8): 337.
Dragunov VP, Neizvestnyy IG, Gridchin VA. Fundamentals of Nanoelectronics. M: Logos. 2006.
Zhukov ND, Gavrikov MV. Technical Physics Letters. 2022; 48: 61-65.
Radantsev VF. Electronic properties of semiconductor nanostructures. Ekaterinburg, 2008; 415. https://elar.urfu.ru/bitstream/10995/1473/7/1334870
Lesovik GB, Sadovskiy IA. Scattering matrix approach to the description of quantum electron transport. Advances in physical sciences. 2011; 181(10): 1041.
Glinskiy GF. Pis'ma v ZHTF. 2018; 44(6): 17.
Utsugi T, Kuno T, Lee N, Tsuchiya R, Mine T, Hisamoto D, Saito S, Mizuno H. Phys Rev B. 2023; 108: 235308.
Reich KV. Conductivity of quantum dot arrays. Advances in Physical Sciences. 2020; 190: 1062-1084. DOI: https: //doi.org/10.3367/UFNr.2019.08.038649
Diaconescu B, Padilha LA, Nagpal P, Swartzentruber BS, Klimov VI. Measurement of electronic states of PbS nanocrystal quantum dots using scanning tunneling spectroscopy: the role of parity selection rules in optical absorption. Phys Rev Lett. 2013 Mar 22;110(12):127406. doi: 10.1103/PhysRevLett.110.127406. Epub 2013 Mar 22. PMID: 25166850.
Zhukov ND, Gavrikov MV, Shtykov SN. Dimensional Modeling of the Synthesis and Conductivity of Colloidal Quantum Dots. Semiconductors. 2022; 56: 269-274.
Zhukov ND, Gavrikov MV, Kabanov VF, Yagudin IT. Semiconductors. 2021; 55: 470–475.
Montanarella F, Kovalenko MV. Three Millennia of Nanocrystals. ACS Nano.2022; 16(4):5085-5102. https://doi.org/10.1021/ acsnano.1c11159
Krylsky DV, Zhukov ND. Technical Physics Letters. 2020; 46: 901–904.
Zhukov ND, Gavrikov MV. MNIZH. 2021; 8(110): 19. https://doi.org/10.23670/IRJ.
Dmitriyev IA, Suris RA. Electron localization and bloch oscillations in quantum-dot superlattices under a constant electric field. Physics and Technology of Semiconductors. Physics and Technology of Semiconductors. 2001; 35(2): 219.
Bagrayev NT, Buravlev AD, Klyachkin LYe, Malyarenko AM, Gel'khoff V, Ivanov VK, Shelykh IA. Physics and Technology of Semiconductors. 2002; 36(4): 462.
Vorob'yev LE, Danilov SN, Zerova VL, Firsov DA. Physics and Technology of Semiconductors. 2003; 37(5):604.
Ivashkin A, Abdurashitov D, Baranov A, Guber F , Morozov S, Musin S, Strizhak A, Tkachev I. Testing entanglement of annihilation photons. Scientific Reports. 2023; 13:7559. https://doi.org/10.1038/s41598-023-34767-8
Fujihashi Y, Shimizu R, Ishizaki A. Probing exciton dynamics with spectral selectivity through the use of quantum entangled photons. PhysicalRev Research. 2020; 2: 023256. DOI: 10.1103/PhysRevResearch.2.023256
Lib O, Hasson G, Bromberg Y. Real-time shaping of entangled photons by classical control and feedback. Sci Adv. 2020; 6: eabb62989.
Patent RU 2777199 “Method of manufacturing a conductive nanocell with quantum dots.” Priority 08/10/2021
Chua, Leon O.Memristor-The missing circuit element. IEEE Transactions on Circuit Theory. 1971; 18: 507-519.
Xiao Y, Jiang B, Zhang Z, Ke S, Jin Y, Wen X, Ye Sci Technol Adv Mater. 2023; 24(1): 2162323. doi: 10.1080/14686996.2022.2162323