
Development of a Mechanical Seal Closed Design Model
Information Technology Mechanical EngineeringReceived 29 Feb 2024 Accepted 19 Feb 2024 Published online 20 Feb 2024
ISSN: 2995-8067 | Quick Google Scholar


Received 29 Feb 2024 Accepted 19 Feb 2024 Published online 20 Feb 2024
The operating experience of mechanical seals shows that as a result of angular deformations of the rings, the wear of the contact surfaces along the radius is uneven. When designing mechanical seals, it is necessary to calculate the amount of expected leakage through the seal, friction power consumption, as well as the possible durability of the unit. These calculated dependencies and estimates are obtained based on the constructed mechanical seal model. In the area of hydrodynamic load support in the case of a confusor joint or a converging film, the slope of the pressure diagram is such that a decrease in the film thickness increases the hydrodynamic support. This is referred to as enabling stable non-contact sealing operation. The execution of the rubbing surfaces of the interface of the end pair should ensure the formation of the calculated confusor shape of the sealing gap in all modes of operation and axisymmetric pressure fields during the rotation of the rotor.
The higher the load level of energy facilities and their power systems, the greater the thermal and mechanical loads that cause deformation of the sealing units of rotary machines [1,2], which creates problems in improving the theoretical basis of their design.
Due to the increase in energy intensity and other parameters of centrifugal machines, their reliability, and, consequently, safety, are determined by shaft seal systems [3,4]. The main difficulties in creating equipment with high parameters are associated with the calculation and design of these components and systems [5,6]. These problems are complicated by the fact that the rotor, together with the shaft seals, represents a single closed hydromechanical system, the performance of which is determined by the properties and interaction of all its elements [7,8].
Despite the apparent simplicity of assembling the mechanical seal, the processes that occur when connecting the mating end surfaces of two parts (one of which rotates with the rotor) are extremely complex [9,10]. This is due to the simultaneous influence and connection of friction processes, hydrodynamics, and thermal processes, as well as changes in the shape of the mating surfaces in the sealing joint when the load parameters of the seal change [11,12].
When designing a conventional mechanical seal, the designer needs relationships to estimate the expected seal leakage, the magnitude of the frictional force, and the likely durability of the assembly [13,14]. These calculated dependencies and estimates can be obtained on the basis of a closed working model containing a mathematical description of the processes occurring in the sealing gap and a given criterion for their optimality [15,16].
The most significant mechanism for the occurrence of the supporting force in the end connection of the seal is the influence of the deviation of the sliding surfaces from parallelism [17]. The reason for such deviations, according to researchers [18,19], may be thermal and mechanical deformations of the sealing surfaces that arise during the operation of the mechanical seal, as well as the initial errors of these surfaces. obtained during operation, finishing operations during the manufacture of rings, or assembly of the sealing unit [20].
Based on the analysis of the physical foundations of the operation of mechanical seals, a model of sealing and bearing capacity is proposed, which allows for solving the problems of designing mechanical seals.
Let us consider the general model of an ordinary mechanical seal, in the contact joint of which, formed by the curved surfaces of the sealing rings, a confusor or diffuser form of the gap is formed in the radial direction.
The most significant mechanism for the occurrence of a support force is the influence of the deviation of sliding surfaces from parallelism.
The transition of a mechanical seal from the stage of rest to the stage of operation with a rotating shaft, up to reaching the nominal speed mode, is associated with a number of processes that usually remain outside the known models describing the operation of mechanical seals. So, in the known models of the mechanical seal operation, only the stationary mode with certain loading parameters becomes the object of description and study without taking into account the influence of the processes preceding this stage [13,20-24].
Let us consider the processes occurring in the sealing gap of a typical unloaded mechanical seal of the pump shaft.
The working process in the mechanical seal from the moment the shaft begins to rotate until the establishment of a stationary mode of operation is associated with the development of a number of non-stationary phenomena in the sealing joint and the body of the seal rings with a gradual transition of the parameters to those established under the nominal mode of operation
After the drive is turned on and the rotating ring begins to move, the sealing work is associated with an increase in the sliding speed and with the non-stationary friction phenomena of the sealing surfaces. Between the surfaces of the rings, initially pressed to each other by the axial force created by the elastic spring elements, during their relative movement — under the conditions of contact interaction — phenomena arise associated with the rejection of the axially movable ring by a certain amount from the surface of the axially stationary ring (due to interaction of the circumferential moment and the braking forces of contact friction between the sealing surfaces of the rings). The initial moment of relative movement of the ring surfaces occurs in conditions of almost complete absence of lubrication between the sealing surfaces. However, frictional forces in the contact surfaces cause frequent axial movement of the axially movable ring, thereby ensuring the flow of lubricant between the sealing surfaces. The friction of the surfaces in individual contact patches leads to heat generation and uneven heating of the rings along the height. The resulting temperature changes on the sealing surfaces of the rings depend on the value of the contact pressure at the junction of the surfaces and the sliding speed in the rubbing pair: where is the peripheral sliding speed in the rubbing pair of rings (variable at the starting stage of the seal operation).
From the impact of a local axial temperature difference in the bodies of the rings, a deformation close to axisymmetric with a slightly pronounced wave-likeness in the circumferential direction occurs with an axial deformation with dimensions of fractions of micrometers, associated with a local rotation of the sections of the rings relative to the longitudinal axis of symmetry in the direction of temperature drop. The appearance of a weakly pronounced wave-likeness of the sealing surfaces of the rings and the number of waves on their outer diameters are the results of the uneven action of forces from individual springs or a single elastic element (central spring, bellows, membrane), from the angle of intersection of the longitudinal axes of the rotating and non-rotating rings, the non-parallelism parameter of the rings sliding, and also on the relative sliding velocity in the friction pair.
There is also a temperature difference across the width of the rings, leading to a local (in fractions of micrometers) rise of the surface of each of the rings near the inner radius of the sealing shoulder. In the end gap, a conical shape with irregular waviness of the conjugation of the sealing surfaces is formed, with a gap size on the outer diameter of the rings in fractions of micrometers and local cavities of the same order of axial dimensions between the sealing surfaces, formed by the resulting unorganized bulges and depressions. The reasons for the appearance of the latter can also be local anisotropy of the materials of the rings, micro waviness obtained during finishing operations, stress relaxation in the bodies of the rings associated with a change in their thermal state, and non-axial symmetry of both the bodies of the sealing rings and the elements of their interface with adjacent parts.
The initial stationary regime of almost dry friction, due to the lubricant entering the cavities formed between the sealing surfaces during their relative displacement, passes into the stage of boundary friction with a continuing increase in the sliding speed and with a gradual decrease in the contact interaction of the surfaces.
The medium to be sealed fills and releases emerging and disappearing cavities removes the generated heat from the sealing surfaces of the rings and heats up itself. With a further increase in the sliding speed in the butt joint, the process of transition from the boundary regime to the regime of semi-fluid friction and the exit of the surfaces from the contact interaction proceeds. These processes are mainly associated with the effect of changing the shape of the sealing surfaces in the circumferential direction and with the phenomenon of throwing off the axially movable ring when the sealing surfaces come into contact. Here, the sources of the formation in a thin layer of lubricant of the carrier hydrodynamic force due to viscous phenomena during the relative movement of the surfaces are local deviations from the flatness of the surfaces in the pair. A bearing force arises due to the wedge effect formed when a flat or convex section of the surface of one ring moves relative to the local convex part of the section formed on the surface of the other ring.
The flow of lubricant in a thin layer between the sealing surfaces is largely due to changes in the angle of intersection of the axes of the rotor and body parts of the seal assembly due to the compliance of the angular position of the axially movable block.
In the absence of pressure drop across the seal or its low level under conditions of low loading of the pair by the axial force created only by spring elements, the resulting bearing force in the gap between the end surfaces is sufficient to ensure non-contact operation of the mechanical seal without wear of the sealing surfaces.
For the hydrodynamic lubrication regime, the lifting force in the gap largely depends on the gap between the relatively moving surfaces (it is proportional to the 5th power of the wedge gap). Thus, a lifting force sufficient to separate the surfaces in the slot is formed even at very small gaps, which are characteristic of the boundary friction regime.
At small gaps and continuing up to reaching the stationary mode of operation, an increase in the relative velocity of sliding of the surfaces of the rings in the friction pair, significant heat generation is formed. This causes a noticeable increase in temperature in the medium that fills the end gap and further deformation of the surfaces forming this gap. The rate of temperature growth in the gap and the rings is significant; the main part of this process takes the first few seconds of the operation of the sealing unit [25].
The temperature of the medium in the sealing gap depends on the circumferential speed of rotation of the shaft, the coefficients of thermal conductivity of the ring materials, the conditions of heat transfer to the medium to be sealed surrounding the seal assembly, and the thermophysical properties of the medium to be sealed.
Under the influence of thermal deformations of the rings, along with the waviness of the sealing surfaces, there is a process of active formation of a gap close to the axisymmetric wedge shape in the radial direction with a maximum opening of the gap from the side of the outer diameters of the rings.
With an increase in the shaft speed, the pressure behind the pump impeller increases, and the pressure drop across the seal increases. The axial load on the sealing joint of the pair and the hydrostatic component in the axial unloading force increase due to the growth of the pressure diagram in the radial direction along the end gap; the hydrodynamic component of the bearing force is reduced. The force deformations, growing in this case from loading the parts of the mechanical seal with the pressure of the medium being sealed in some seal designs, can be significant and even exceed the deformations from temperature phenomena. The direction of action of force deformations in the vast majority of cases (due to the design features of the execution of parts of mechanical seal units) is associated with the rotation of the cross-section of the rings in the direction opposite to that which was the result of temperature deformations from the axial temperature gradient.
In the entire time interval of the mechanical seal reaching the nominal operating mode, the friction surfaces are running in, associated with an increase in the supply of lubrication to the rubbing surfaces in accordance with the loading conditions of the end pair. The lubricating layer thickness between the sealing surfaces of the rings grows. With the formation of a sufficient supply of lubricant to the rubbing surfaces in the end pair, the stage of liquid friction begins.
The main influencing factors on the magnitude of the bearing force are the flow of lubricant in the radial direction and the radial shape of the gap between the end surfaces of the rings, as well as the non-parallelism of the sliding of their sealing surfaces. Local deviations in the circumferential irregularity of the shape of the surfaces of the rings cease to be a significant source of bearing force due to the radial spreading of the lubricating layer due to the narrow width of the sealing collar. The bearing force in the liquid layer becomes quasi-stable and is in equilibrium with the force loading the axially movable block. This balance is maintained due to the current change in the minimum size of the gap in the approach of the surfaces, as well as by increasing or decreasing the current taper of the gap in the radial and circumferential directions due to the non-parallel sliding of the sealing surfaces. This is ensured mainly by compliance with the angular displacement of the axially movable block. The scheme of the end gap of the sealing unit after it enters the liquid friction mode with the decisive influence of hydrostatic forces is shown in Figure 1.
Now the greatest influence on the value of the bearing force between the end surfaces is exerted by the value of the average gap between the sealing surfaces.
Studies have shown that a change in the circumferential direction of the non-parallelism parameter of the sealing surfaces within the average gap size can affect the bearing force in sizes up to 40% of the loading force. Thus, the change in the non-parallelism of the sealing surfaces in the end joint of the rings is a powerful factor influencing the bearing force.
With an already established fluid friction mode, current changes in loading modes (for example, pressure, coolant flow rate, etc.) can change the lubrication conditions in the sealing gap. So, insufficient heat removal from the rings, the unfavorable nature of their force deformations, leading to the formation of a diffuser shape of the sealing gap, or insufficient angular compliance of the axially movable block of the seal assembly (due to a decrease in the elastic properties of the secondary sealing elements or insufficient gaps in the mating of parts) can cause a significant change in the nature of the lubrication of the sealing surfaces [26].
These changes are the result of overheating of the lubricant layer in the sealing gap, a drop in the viscosity properties of this layer and the associated increasing convergence and contacts of the surfaces, the occurrence of semi-dry and dry friction processes in the sealing gap.
Further development of processes in the sealing gap, even before reaching the stationary mode of operation or already in the stationary area of operation with changes in the parameters of the nominal operating mode, can proceed according to three schemes:
– The transition of the mechanical seal to the contact mode of operation with dry or mixed friction;
– Operation of the mechanical seal in the non-contact liquid hydrostatic mode of friction in the lubricating layer between the sealing surfaces in the end gap;
– Operation of the mechanical seal with cyclic transitions from non-contact to contact mode and vice versa.
The operation of an ordinary mechanical seal according to the first scheme is typical for cases of supercritical deviations of parameters from those already established and providing a favorable hydrodynamic lubrication regime. This may be due to a deterioration in the quality of cooling of the sealing unit, with a change in the dynamic properties of the “rotor-axially movable ring” system.
The operation of the mechanical seal according to the second scheme makes it possible to obtain a long-term performance of the assembly, low leakage rates, and friction power costs when sealing medium and high-pressure drops. To describe the mathematical model and obtain the necessarily calculated dependences in the stationary mode, a well-developed section of the theory of lubrication can be used [27,28].
The operation of the mechanical seal, according to the third scheme, is one of the most frequently encountered in practice. Such a scheme of operation is common for low-loaded seal assemblies, and for medium-loaded seals, it is associated with current changes in loading modes in terms of pressure, rotor speed, or assembly cooling. The existence of such a scheme of work is associated with frequently arising issues of wear of the sealing pair rings and low current working life of the mechanical seal assembly — in cases where there are no strict requirements for maintaining the routine parameters of the assembly during operation.
The cause of unstable deformation of the sealing gap can also be dynamic loads. For example, vibrations of a rotor can cause bending oscillations of its axis [29] and the corresponding evolution of the sealing surface of a rotating ring.
When the pump drive is turned off, the end of the mechanical seal operation begins with a gradual decrease in the sliding speed and a drop in the pressure drop across the seal. In the gap, the fluid mode of friction is still preserved; however, the process of changing the radial profile of the shape of the slot, in the direction of decreasing confusion due to a decrease in temperature and force deformations, is underway the role of axial force from the elastic element of the compression of the rings increases; the convergence of the sealing surfaces of the rings increases.
There is a local contact of these surfaces along the tops of the waviness, and the number of contacts increases. The stage of liquid friction passes into semi-fluid and then into boundary friction. The deformation of the rings due to force factors disappears, and the nature of the deformation is determined by the temperature inhomogeneity in the bodies of the rings. There comes a stage of semi-dry sliding of surfaces with contact interaction of surfaces and with an accelerated drop in the sliding speed. The rotating seal ring stops. This is the general picture of the working process of an ordinary mechanical seal.
Let us consider in more detail the processes occurring in the second, most favorable, and economically feasible scheme of the mechanical seal.
It is possible to determine what the minimum gap, in the end, will be when the mechanical seal is operating in the design mode by the force loading of the end joint and the given leakage, as well as by the shape of the end sealing gap.
The determination of the calculated dependences for the end gap in the hydrodynamic theory of lubrication for narrow slots is based on the joint solution of the system of differential equations of motion of the working fluid, the continuity of the lubricant flow, the state, and energy that describes the hydro- and thermodynamic processes in the tract and changes in the parameters of the system motion.
Due to the complexity of the initial differential equations, a number of generally accepted assumptions are made, due both to the peculiarities of the operation of seals and to simplifications that do not significantly affect the accuracy of the results obtained but greatly facilitate computational work:
1. The flow of the working fluid in the slot is assumed to be isothermal — it is based on the fact that when the mechanical seal operates in the liquid friction mode, there is intense heat transfer from the lubricating layer to the rings and, therefore, the temperature of the lubricating layer in the gap can be averaged without much error. This approach is also supported by experimental data [26].
2. The pressure of the working fluid does not change along the layer thickness — it is based on the smallness of the contribution to the pressure change of inertial forces in the lubricating layer compared to the forces of viscosity when the mechanical seal operates in the liquid friction mode.
3. The laminar flow regime of the medium is realized in the sealing gap — it is based on the fact that when the mechanical seal operates in the liquid friction mode, with current operating clearances and the loading pressure drops, only the laminar flow regime of the medium being sealed.
4. Changes in the gap per revolution of the ring are averaged — based on the fact that after the mechanical seal reaches the design mode of operation, it is considered as steady with stable parameters.
We take the following as initial conditions:
– Liquid medium pressure p1 in the seal chamber is equal to atmospheric pressure;
– Differential pressure across the seal is 0;
– Contact pressure
at the joint of the sealing surfaces of the rings is determined by the force of the elastic elements Fn and the nominal contact area S
– The temperature in the seal rings is equal to the temperature of the medium being sealed Tk = Tc.
Since the changes in the viscosity of the medium being sealed in the gap due to temperature are insignificant, the effect of changes in the temperatures of the medium along the gap on the pressure distribution can be neglected, and the energy equation cannot be introduced into the system of equations describing the processes in the end gap of the seal. The system of equations for the stationary case of a laminar flow of a medium through an end gap (formed by smooth surfaces) as applied to mechanical seals can be written as a continuity equation:
, (1)
And the equations of fluid motion — due to the assumption of constant pressure across the thickness of the lubricating layer — can be represented in the form of a system of Reynolds equations:
(2)
;
With boundary conditions:
(3)
Which for Newtonian fluids represent the kinematic conditions on the walls limiting the investigated flow (here φ is the displacement angle of the rotating ring along the angular coordinate, Figure 1).
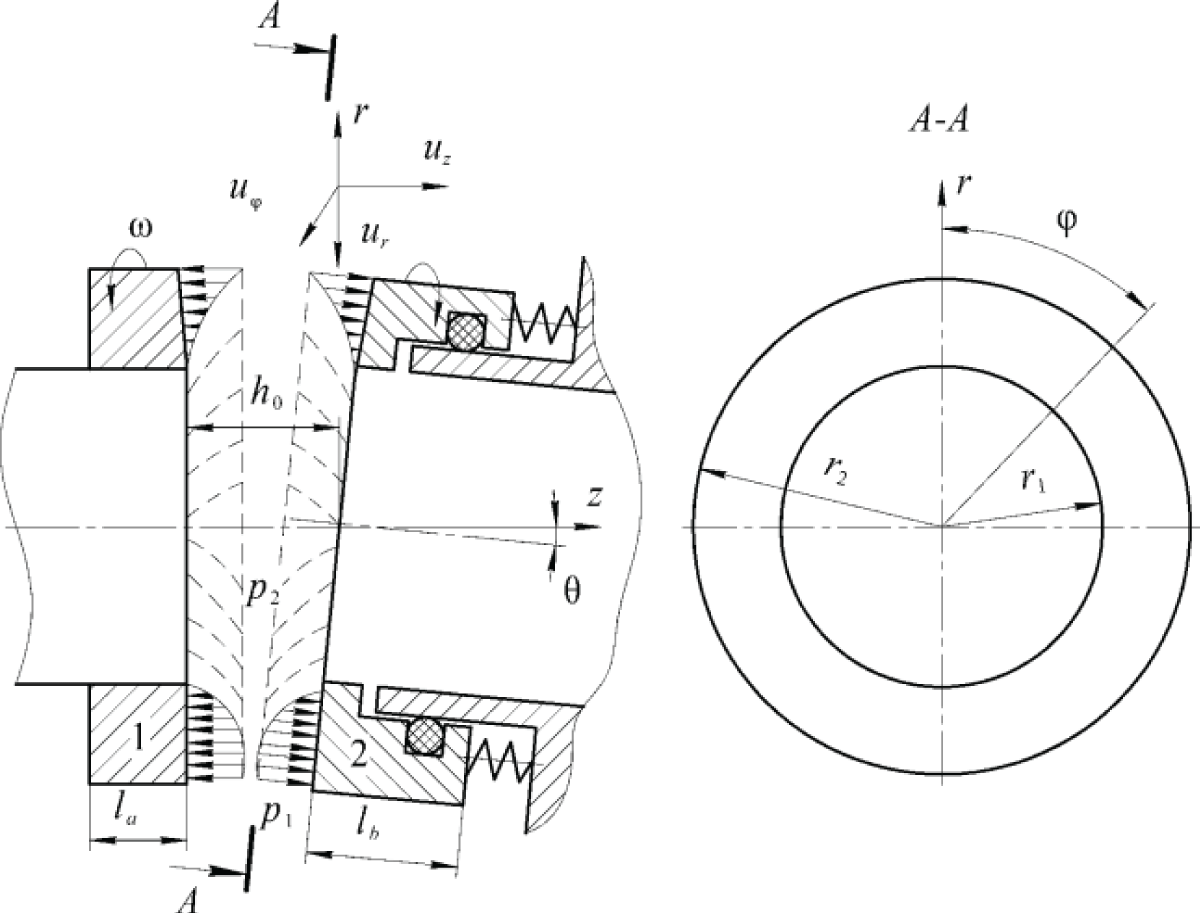 Figure 1: Scheme of the end gap of the sealing unit after it enters the liquid friction mode with the determining influence of hydrostatic forces.
Let’s introduce the following definitions:
r, z, are radial, axial, and angular coordinates;
u,r, u,z, u,φ are the radial, axial, and angular velocities of the medium flow;
ω is the angular velocity of rotation of the ring;
p1, p2 - pressure before and after the seal;
Fn is the force of the elastic spring element;
h0 - the average gap between the sealing surfaces;
la, lb are the body heights of ring A and ring B, respectively;
θ - the angle of non-parallelism of the sealing surfaces of the rings;
r1, r2 - inner and outer radii of the sealing surfaces of the rings.
Figure 1: Scheme of the end gap of the sealing unit after it enters the liquid friction mode with the determining influence of hydrostatic forces.
Let’s introduce the following definitions:
r, z, are radial, axial, and angular coordinates;
u,r, u,z, u,φ are the radial, axial, and angular velocities of the medium flow;
ω is the angular velocity of rotation of the ring;
p1, p2 - pressure before and after the seal;
Fn is the force of the elastic spring element;
h0 - the average gap between the sealing surfaces;
la, lb are the body heights of ring A and ring B, respectively;
θ - the angle of non-parallelism of the sealing surfaces of the rings;
r1, r2 - inner and outer radii of the sealing surfaces of the rings.
Integrating the system of equations (2) with respect to z under boundary conditions (3), we obtain the generalized Reynolds lubrication equation:
(4)
Restricting ourselves to considering the axisymmetric problem only for radial flow in the end gap, according to the above-described picture of processes for the design mode in the sealing joint and neglecting the effect of compression of the medium film in the gap, we obtain expression (4) in the form:
(5)
The unknowns here are the gap change and the current pressure change in the radial direction.
For isothermal flows of the medium, the necessary additional relations for solving the equations are the pressure dependences of the viscosity μ and density ρ of the medium. Restricting ourselves to the consideration of the operation of a mechanical seal for a liquid in the region of medium pressures, we set μ(p) = const and ρ(р) = const.
To evaluate the efficiency of the calculated mechanical seal, the following design characteristics are required: leakage Q through the seal, power consumption N for its operation, and long-term performance of the assembly, which can be guaranteed only by the non-contact operation of the sealing pair.
The optimization parameter (which, as a given basic criterion, the designer needs to focus on when designing the sealed unit) can be the maximum rigidity of the liquid layer in the sealing gap, associated with the shape of the gap itself and the characteristics of the medium being sealed [30,31].
Integrating (5) over r, using in the solution the substitution , an intermediate solution when integrating systems (1), (2), and introducing dimensionless quantities, we obtain the system of equations:
(6)
Here, is the dimensionless centrifugal parameter of the gap; ρ* is the base (initial) value of the density of the medium; Δp = p1 – p2 is the pressure drop across the seal.
Introducing a new variable , we integrate system (6) under boundary conditions:
The solution to the problem can be represented as:
(7)
, (8)
where is the hydrostatic bearing force in the gap;
F* is the base value of the bearing force.
To determine the moment of friction , it is necessary to integrate elementary moments from shear stresses over the area of the gap:
After transformations in dimensionless form, we have
. (9)
In dimensional form , where
The obtained dependences (4) — (7) allow us to determine the main characteristics of the mechanical seal: leakage, bearing force in the gap, friction moment, and pressure diagram.
Due to the fact that during the operation of a mechanical seal, the absence of axial symmetry of the annular gap is possible due to the non-parallelism of the rubbing surfaces of the rings (Figure 1), the use of formulas (7), (8) and (9), obtained under the assumption of axisymmetric flow, may be illegal, since for these conditions it becomes necessary to consider a three-dimensional problem.
However, with a small change in the gap in the circumferential direction, when the radial pressure gradient is much greater than the circumferential one, the effect of non-parallelism of the surfaces of the rings in the friction pair can be taken into account in the first approximation based on the fact that the values dMF, dF and dQ for each elementary annular sector with an angle d φ can be determined by the formulas (7), (8) and (9) for the current value of the radial gap. By integrating the obtained solutions for elementary ring sectors, one can obtain generalizing partial solutions of the characteristics MF, F, and Q for a number of axisymmetric approaches of the surfaces of a sealing pair of rings.
Consider the options for the mutual arrangement of the sealing surfaces of the mechanical seal rings (Figure 2).
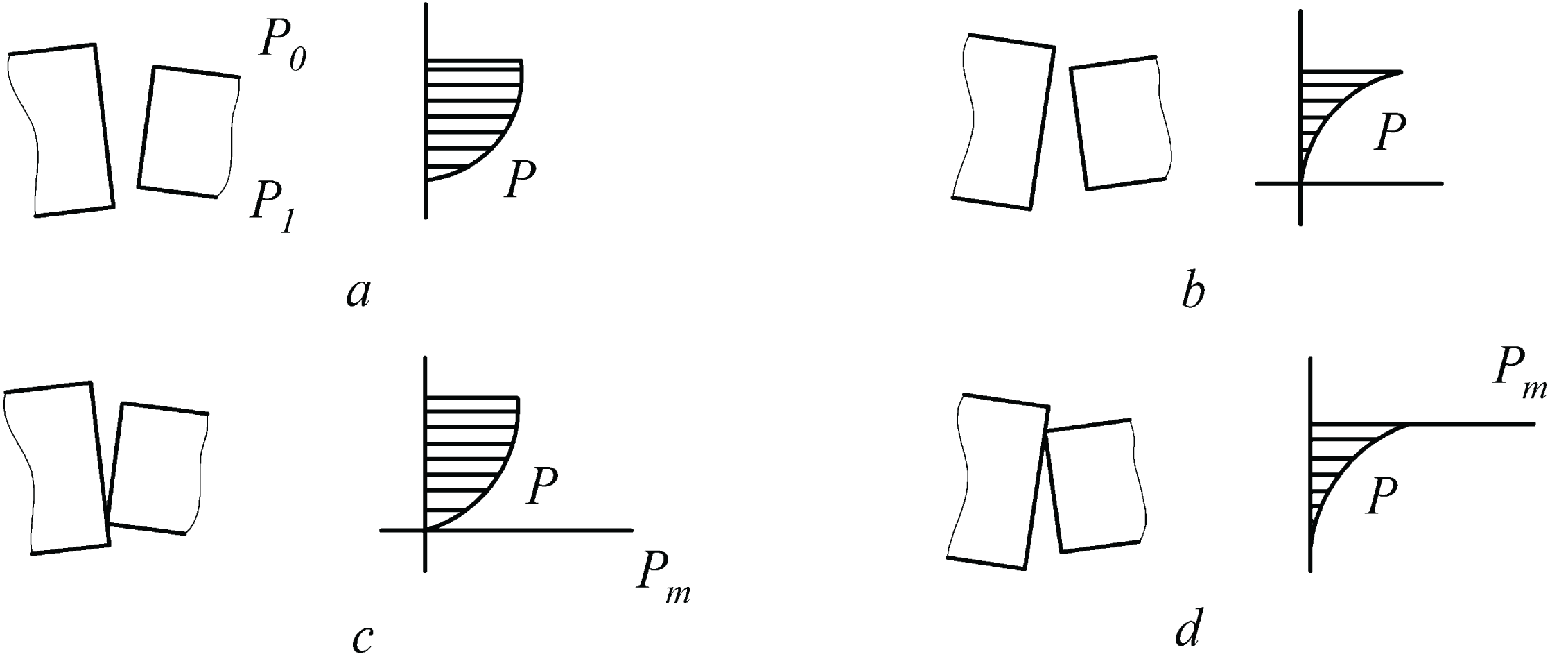 Figure 2: The location of the sealing surfaces of the mechanical seal rings and the diagram of the pressure of the sealed liquid: a - Confusor open joint, b - Diffuser open joint, c - Confusor joint with contact, d - Diffuser joint with contact.
Figure 2: The location of the sealing surfaces of the mechanical seal rings and the diagram of the pressure of the sealed liquid: a - Confusor open joint, b - Diffuser open joint, c - Confusor joint with contact, d - Diffuser joint with contact.
In the first case (Figure 2a) there is no contact between the sealing surfaces, so the force that opens the joint is created due to fluid pressure in the gap. As the fluid pressure plot for this case shows, the average fluid pressure is somewhat greater than the average of the internal and external pressures. For the case of a diffuser open joint (Figure 2b), the pressure in the film is less than the average value of the internal and external pressures. This case is not stable and will result in contact between the rings as shown in Figure 2d. Fluid pressure distribution diagrams in cases of contact between the rings, shown in Figure 2c, 2d will take extreme forms as the minimum film thickness approaches zero. Thus, the total possible change in the magnitude of the load created by the pressure of the liquid, when moving from a fully divergent (confusor) joint to a fully convergent (diffuser) joint, ranges from zero to a pressure equal to the pressure being sealed. Since in practical cases, the film thickness cannot be zero due to roughness, these limits cannot be reached.
In the last two cases shown in Figure 2, contact occurs in the presence of a radial cone. For these cases, the concentrated contact load acts either inside or outside, depending on the direction of the radial cone.
The results of the analysis show that after the seal reaches a stationary mode, a stable lubricating layer is formed between the sealing surfaces in the end gap and the seal operates in the liquid hydrostatic friction mode. The shape of the end gap has a great influence on the characteristics of the lubricant film in the friction pair. In the area of hydrodynamic load support in the case of a tapering joint or converging film, the slope of the pressure diagram is such that reducing the film thickness increases the hydrodynamic support. This ensures positive stiffness and stable non-contact seal operation. If the joint is divergent (diffusor), then the pressure diagram has negative rigidity and provides unstable load support. In this case, the film is destroyed and the seal operates in contact mode, i.e., the non-contact expanding film is unstable.
In order to ensure the successful development of mechanical seal assemblies, it is necessary to calculate the deformations of the sealing rings caused by both the pressure of the sealing medium and thermal effects in order to predict the size and direction of the radial cone and avoid unstable seal operation.
The mechanism of the appearance of a lubricant film between the rings of the mechanical seal’s end pair has not yet been studied enough, this opens a wide field for further research.
The methods developed and presented in the article for calculating the heat generation and deformation of the rings of a sealing pair makes it possible to obtain the geometric parameters of the seal with sufficient accuracy for practice, ensuring the required performance characteristics. This is especially important for highly loaded high-speed centrifugal machines, during the operation of which a large heat generation occurs in the end sealing grooves.
Shevchenko S. Development of a Mechanical Seal Closed Design Model. IgMin Res. 20 Feb, 2024; 2(2): 113-120. IgMin ID: igmin152; DOI: 10.61927/igmin152; Available at: www.igminresearch.com/articles/pdf/igmin152.pdf
Anyone you share the following link with will be able to read this content:
Address Correspondence:
Serhii Shevchenko, Pukhov Institute for Modelling in Energy Engineering, General Naumov Str. 15, 03164 Kyiv, Ukraine, Email: [email protected]
How to cite this article:
Shevchenko S. Development of a Mechanical Seal Closed Design Model. IgMin Res. 20 Feb, 2024; 2(2): 113-120. IgMin ID: igmin152; DOI: 10.61927/igmin152; Available at: www.igminresearch.com/articles/pdf/igmin152.pdf
Copyright: © 2024 Shevchenko S. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
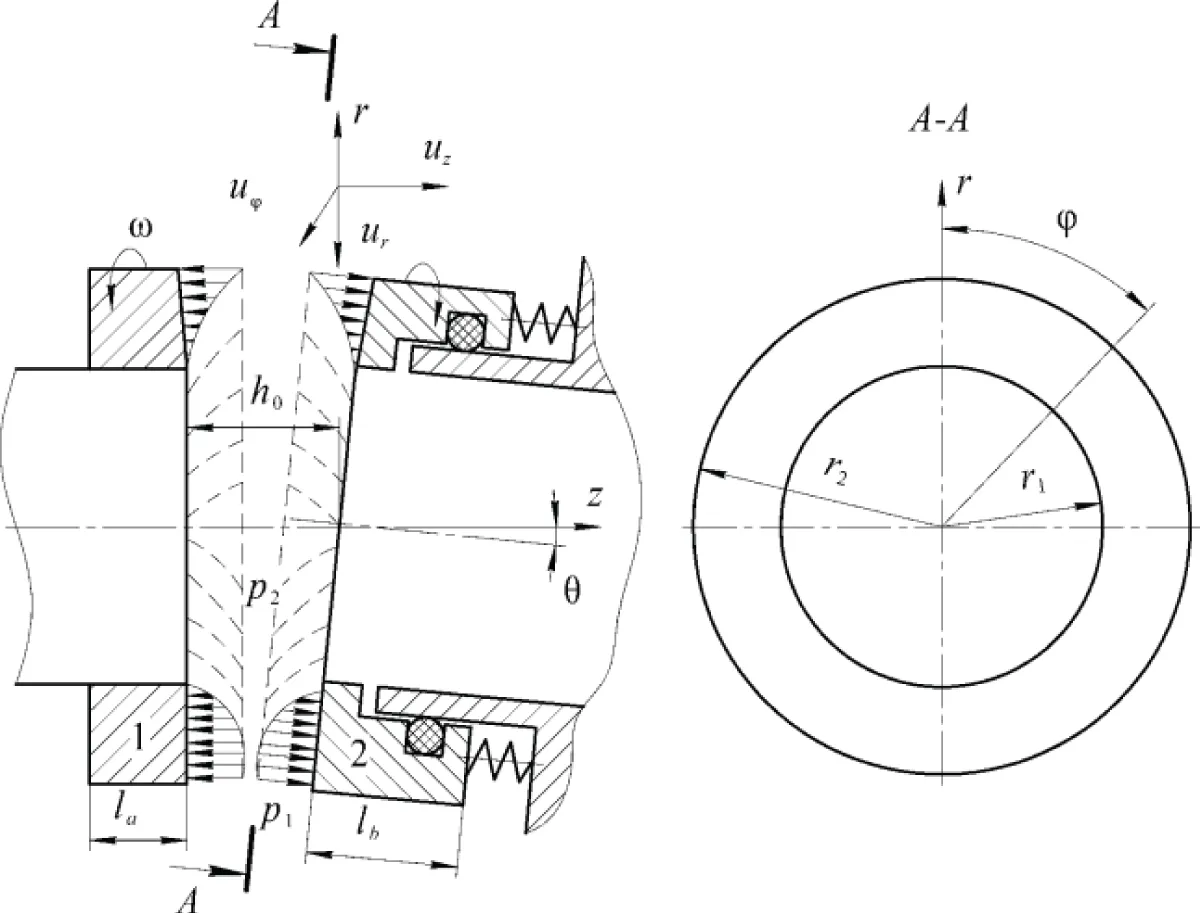 Figure 1: Scheme of the end gap of the sealing unit after it...
Figure 1: Scheme of the end gap of the sealing unit after it...
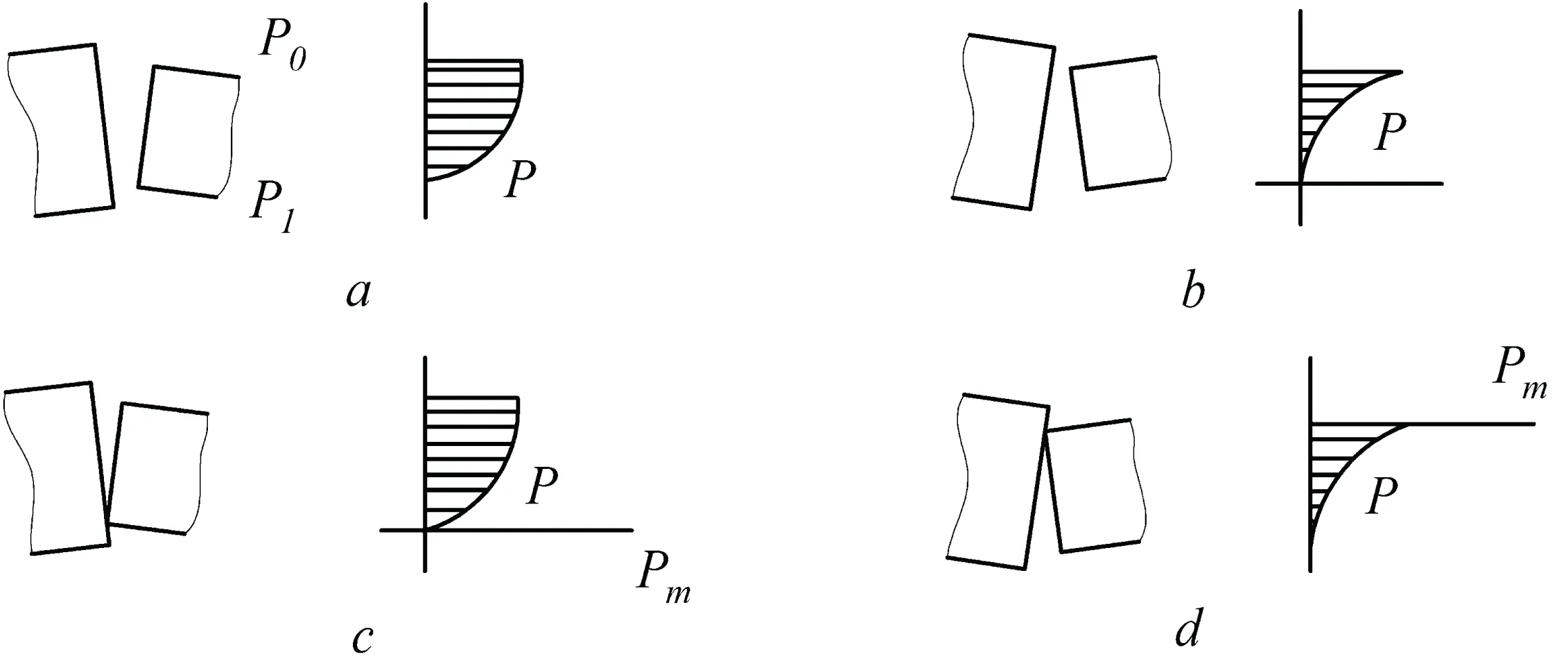 Figure 2: The location of the sealing surfaces of the mechan...
Figure 2: The location of the sealing surfaces of the mechan...
 Figure 1: Scheme of the end gap of the sealing unit after it...
Figure 1: Scheme of the end gap of the sealing unit after it...
 Figure 2: The location of the sealing surfaces of the mechan...
Figure 2: The location of the sealing surfaces of the mechan...
 Figure 1: Scheme of the end gap of the sealing unit after it...
Figure 1: Scheme of the end gap of the sealing unit after it...
 Figure 2: The location of the sealing surfaces of the mechan...
Figure 2: The location of the sealing surfaces of the mechan...